Globally symmetric Riemannian space
A Riemannian manifold 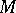 each point
each point 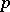 of which is an isolated fixed point of some involutory isometry
of which is an isolated fixed point of some involutory isometry 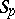 of
of 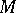 , i.e.
, i.e. 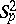 is the identity transformation. Let
is the identity transformation. Let 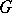 be the component of the identity in the group of isometries of the space
be the component of the identity in the group of isometries of the space 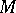 and let
and let 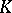 be the isotropy subgroup at the point
be the isotropy subgroup at the point 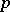 . Then
. Then 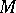 is the homogeneous space
is the homogeneous space 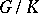 , and the mapping
, and the mapping 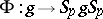 is an involutory automorphism of
is an involutory automorphism of 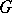 ; moreover,
; moreover, 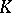 is contained in the closed subgroup
is contained in the closed subgroup 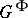 of all fixed points of
of all fixed points of  and contains the component of the identity in
and contains the component of the identity in 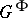 .
.
Let 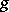 be a real Lie algebra, let
be a real Lie algebra, let 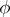 be an involutory automorphism of it and let
be an involutory automorphism of it and let 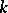 be the subalgebra in
be the subalgebra in  of all
of all  -fixed elements. Consider the connected subgroup
-fixed elements. Consider the connected subgroup  of the associated group
of the associated group 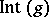 corresponding to the subalgebra
corresponding to the subalgebra 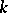 . If the group
. If the group 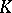 is compact, then
is compact, then 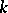 is called a compactly-imbedded subalgebra of
is called a compactly-imbedded subalgebra of 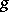 , while the pair
, while the pair 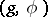 is known as an orthogonal symmetric Lie algebra. Let
is known as an orthogonal symmetric Lie algebra. Let 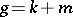 be the decomposition into the eigen subspaces of
be the decomposition into the eigen subspaces of 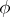 corresponding to the eigen values 1 and
corresponding to the eigen values 1 and 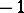 . The pair
. The pair 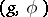 is known as: a) an algebra of compact type if
is known as: a) an algebra of compact type if  is compact and semi-simple; b) an algebra of non-compact type if
is compact and semi-simple; b) an algebra of non-compact type if 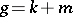 is a Cartan decomposition; and c) an algebra of Euclidean type if
is a Cartan decomposition; and c) an algebra of Euclidean type if 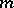 is an Abelian ideal in
is an Abelian ideal in 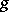 . Let
. Let 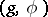 be an orthogonal symmetric Lie algebra and let
be an orthogonal symmetric Lie algebra and let 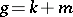 be the above decomposition. Denote by
be the above decomposition. Denote by 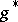 the subset
the subset 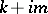 of the complex hull
of the complex hull 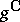 of
of  . The mapping
. The mapping
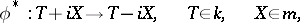 |
is an involutory automorphism of the algebra  , and
, and  is an orthogonal symmetric Lie algebra, called the dual to
is an orthogonal symmetric Lie algebra, called the dual to  . If
. If  is an algebra of compact type, then
is an algebra of compact type, then  is an algebra of non-compact type and vice versa.
is an algebra of non-compact type and vice versa.
Each globally symmetric Riemannian space  generates an orthogonal symmetric Lie algebra
generates an orthogonal symmetric Lie algebra 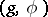 , where
, where 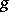 is the Lie algebra of the group
is the Lie algebra of the group 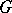 and
and  (
( is the identity in the group).
is the identity in the group). 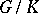 is called a space of compact or non-compact type, depending on the type of the pair
is called a space of compact or non-compact type, depending on the type of the pair 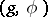 it generates. All simply-connected globally symmetric Riemannian spaces
it generates. All simply-connected globally symmetric Riemannian spaces 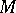 are direct products:
are direct products:  , where
, where  is a Euclidean space, and
is a Euclidean space, and 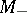 and
and 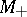 are globally symmetric Riemannian spaces of compact and non-compact types, respectively. For any space of non-compact type the curvature is non-positive in any two-dimensional direction; this curvature is everywhere non-negative for spaces of compact type. Any space of non-compact type is diffeomorphic to a Euclidean space.
are globally symmetric Riemannian spaces of compact and non-compact types, respectively. For any space of non-compact type the curvature is non-positive in any two-dimensional direction; this curvature is everywhere non-negative for spaces of compact type. Any space of non-compact type is diffeomorphic to a Euclidean space.
Let 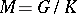 be a globally symmetric Riemannian space of compact or non-compact type. The rank
be a globally symmetric Riemannian space of compact or non-compact type. The rank 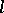 of
of 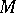 is the maximal dimension of a flat totally-geodesic submanifold in
is the maximal dimension of a flat totally-geodesic submanifold in 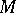 . Let
. Let 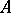 and
and 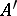 be two flat totally-geodesic submanifolds of
be two flat totally-geodesic submanifolds of 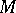 of dimension
of dimension 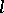 , let
, let 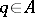 ,
, 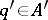 , and let
, and let 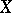 be the tangent vector to
be the tangent vector to 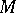 at the point
at the point 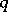 . In such a case: 1) there exists an element
. In such a case: 1) there exists an element 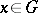 such that
such that  and
and 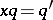 ; and 2) there exists an element
; and 2) there exists an element  such that
such that 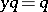 and
and 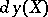 is the tangent vector to
is the tangent vector to 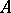 at
at 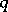 .
.
Let 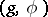 be an orthogonal symmetric Lie algebra and let
be an orthogonal symmetric Lie algebra and let 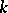 and
and 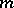 be the eigen subspaces of
be the eigen subspaces of 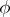 corresponding to the eigen values 1 and
corresponding to the eigen values 1 and 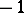 . The algebra
. The algebra  is called irreducible if the following conditions are satisfied: 1)
is called irreducible if the following conditions are satisfied: 1) 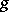 is a semi-simple algebra and
is a semi-simple algebra and 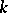 does not contain non-zero ideals of
does not contain non-zero ideals of  ; and 2) the algebra
; and 2) the algebra 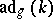 acts irreducibly on
acts irreducibly on 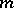 . A globally symmetric Riemannian space
. A globally symmetric Riemannian space 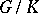 is called irreducible if the orthogonal symmetric Lie algebra
is called irreducible if the orthogonal symmetric Lie algebra 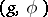 generated by
generated by 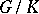 is irreducible. Two orthogonal symmetric Lie algebras
is irreducible. Two orthogonal symmetric Lie algebras 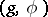 and
and 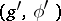 are called isomorphic if there exists an isomorphism
are called isomorphic if there exists an isomorphism 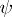 of the algebra
of the algebra 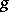 onto
onto 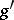 such that
such that 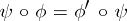 . The classification of simply-connected irreducible globally symmetric Riemannian spaces up to an isometry is equivalent to the classification of irreducible orthogonal symmetric Lie algebras up to an isomorphism.
. The classification of simply-connected irreducible globally symmetric Riemannian spaces up to an isometry is equivalent to the classification of irreducible orthogonal symmetric Lie algebras up to an isomorphism.
The irreducible orthogonal symmetric Lie algebras of compact type are: I. 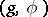 , where
, where 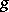 is a compact simple Lie algebra and
is a compact simple Lie algebra and 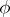 is any of its involutory automorphisms; II.
is any of its involutory automorphisms; II.  , where the compact algebra
, where the compact algebra 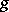 is a direct sum of two simple ideals that are conjugate through the automorphism
is a direct sum of two simple ideals that are conjugate through the automorphism 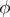 .
.
The irreducible orthogonal symmetric Lie algebras of non-compact type are: III. 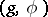 , where
, where  is a simple non-compact Lie algebra over
is a simple non-compact Lie algebra over 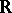 whose complex hull
whose complex hull 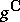 is a simple Lie algebra over
is a simple Lie algebra over 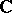 and
and 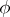 is an involutory automorphism of
is an involutory automorphism of 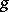 such that its fixed points constitute a maximal compactly-imbedded subalgebra; IV.
such that its fixed points constitute a maximal compactly-imbedded subalgebra; IV. 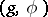 , where
, where  is a simple Lie algebra over
is a simple Lie algebra over 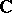 considered as a real Lie algebra and
considered as a real Lie algebra and  is the conjugation of
is the conjugation of 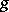 with respect to a maximal compactly-imbedded subalgebra
with respect to a maximal compactly-imbedded subalgebra 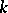 , i.e. a mapping
, i.e. a mapping  ,
,  . Moreover, if
. Moreover, if 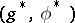 denotes the algebra dual to
denotes the algebra dual to 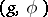 , then the latter is of type III or IV if
, then the latter is of type III or IV if 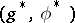 is, respectively, of type I or II, and vice versa.
is, respectively, of type I or II, and vice versa.
Only one globally symmetric Riemannian space is connected with each irreducible orthogonal symmetric algebra of non-compact type, and this space is simply connected. As regards compact algebras, the solution of the corresponding problem is much more complicated. It is sufficient to consider globally symmetric Riemannian spaces of type I and type II, connected with algebras of type II — these are in fact connected compact simple Lie groups endowed with a Riemannian structure which is invariant under left and right translations. The problem of classifying globally symmetric Riemannian spaces connected with algebras of type I, up to local isometries, is equivalent to the problem of classifying involutory automorphisms of simple compact Lie algebras. The global classification of the symmetric Riemannian spaces connected with a given orthogonal symmetric algebra 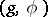 of compact type is solved by the following theorem.
of compact type is solved by the following theorem.
Let 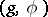 be an orthogonal symmetric algebra of compact type, where the subalgebra
be an orthogonal symmetric algebra of compact type, where the subalgebra 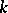 of fixed points of
of fixed points of 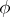 contains no ideals of
contains no ideals of 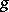 other than
other than 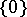 . Let
. Let 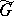 be a simply-connected Lie group with Lie algebra
be a simply-connected Lie group with Lie algebra 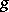 , let
, let  be the centre of
be the centre of 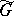 , let
, let 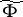 be an automorphism of
be an automorphism of 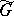 such that
such that 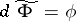 , and let
, and let 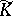 be the set of fixed points of
be the set of fixed points of 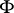 . For an arbitrary subgroup
. For an arbitrary subgroup  of
of  one puts
one puts 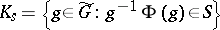 . The globally symmetric Riemannian spaces
. The globally symmetric Riemannian spaces 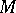 connected with
connected with 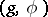 coincide with the spaces of the form
coincide with the spaces of the form 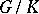 where
where 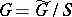 ,
, 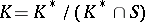 , endowed with an arbitrary
, endowed with an arbitrary 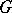 -invariant metric. Here
-invariant metric. Here 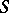 runs through all subgroups of
runs through all subgroups of 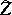 , while
, while 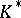 runs through all subgroups of
runs through all subgroups of 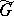 for which
for which 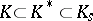 .
.
References
| [1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
| [2] | O. Loos, "Symmetric spaces" , 1–2 , Benjamin (1969) |
Globally symmetric Riemannian space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Globally_symmetric_Riemannian_space&oldid=13064