Quasi-informational extension
of a non-cooperative game 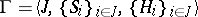
A non-cooperative game 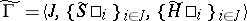 for which mappings
for which mappings 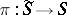 and
and 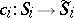 ,
, 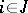 , are given that satisfy the following conditions for all
, are given that satisfy the following conditions for all 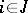 ,
, 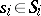 ,
, 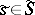 : 1)
: 1) 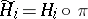 ; and 2)
; and 2) 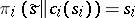 , where
, where  is the composite of
is the composite of 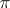 and the projection
and the projection 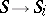 . A quasi-informational extension of the game
. A quasi-informational extension of the game 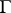 can be interpreted as the result of setting up the above scheme of interaction of players in the choice process for their strategies
can be interpreted as the result of setting up the above scheme of interaction of players in the choice process for their strategies 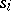 in
in 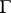 . The strategies
. The strategies 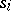 correspond to the rules determining the behaviour of player
correspond to the rules determining the behaviour of player 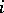 in any situation that he or she may encounter. The mapping
in any situation that he or she may encounter. The mapping 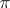 associates the rule of behaviour of the players with a realization of them, that is, with the set of strategies
associates the rule of behaviour of the players with a realization of them, that is, with the set of strategies 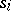 ,
, 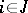 , that will be chosen by the players adhering to the given rules. Condition 1) of the definition of a quasi-informational extension is then the definition of the pay-off function of the new game
, that will be chosen by the players adhering to the given rules. Condition 1) of the definition of a quasi-informational extension is then the definition of the pay-off function of the new game 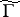 , while condition 2) expresses the preservation by each player of the old strategies
, while condition 2) expresses the preservation by each player of the old strategies 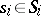 .
.
A situation 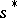 of
of 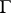 is the image of the equilibrium situation of some quasi-informational extension
is the image of the equilibrium situation of some quasi-informational extension 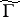 of
of 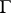 under the corresponding mapping
under the corresponding mapping 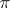 if and only if for any
if and only if for any 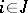 and
and 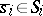 there is a situation
there is a situation 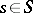 such that
such that
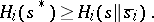 |
The notion of a quasi-informational extension is particularly widely used in the theory of games with a hierarchy structure (cf. Game with a hierarchy structure), where the informal problem of optimizing an informational scheme is transformed into the problem of constructing a quasi-informational extension of a given game providing the first player with an optimum result. One also considers classes of quasi-informational extensions satisfying conditions that express some or other restrictions on the information available to the players. For example, if 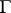 is a
is a  -person game
-person game 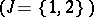 , then one says that in the quasi-informational extension player 1 does not possess (proper) information about the strategy
, then one says that in the quasi-informational extension player 1 does not possess (proper) information about the strategy 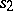 if for each
if for each 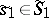 there is an
there is an 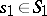 such that
such that 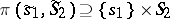 . The best of the quasi-informational extensions satisfying this condition is, for example, "game G3" , whereas the best of the quasi-informational extension is "game G2" .
. The best of the quasi-informational extensions satisfying this condition is, for example, "game G3" , whereas the best of the quasi-informational extension is "game G2" .
References
| [1] | Yu.B. Germeier, "Non-antagonistic games" , Reidel (1986) (Translated from Russian) |
| [2] | N.S. Kukushkin, V.V. Morozov, "The theory of non-antagonistic games" , Moscow (1977) pp. Chapt. 2 (In Russian) |
Quasi-informational extension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-informational_extension&oldid=13056