Covariant tensor
of valency 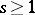
A tensor of type  , an element of the tensor product
, an element of the tensor product 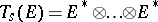 of
of  copies of the dual space
copies of the dual space 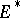 of the vector space
of the vector space 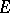 over a field
over a field 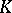 . The space
. The space 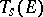 is itself a vector space over
is itself a vector space over  with respect to the addition of covariant tensors of the same valency and multiplication of them by scalars. Let
with respect to the addition of covariant tensors of the same valency and multiplication of them by scalars. Let  be finite dimensional, let
be finite dimensional, let  be a basis of
be a basis of 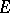 and let
and let  be the basis dual to it of
be the basis dual to it of 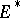 . Then
. Then 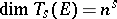 and the set of all tensors of the form
and the set of all tensors of the form  ,
, 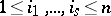 , forms a basis for
, forms a basis for 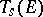 . Any covariant tensor can be represented in the form
. Any covariant tensor can be represented in the form 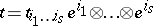 . The numbers
. The numbers 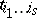 are called the coordinates, or components, of the covariant tensor relative to the basis
are called the coordinates, or components, of the covariant tensor relative to the basis  of
of 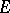 . Under a change of a basis of
. Under a change of a basis of 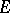 according to the formulas
according to the formulas 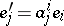 and the corresponding change of the basis of
and the corresponding change of the basis of 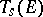 , the components of the covariant tensor
, the components of the covariant tensor  are changed according to the so-called covariant law
are changed according to the so-called covariant law
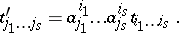 |
If 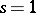 , the covariant tensor is called a covariant vector; when
, the covariant tensor is called a covariant vector; when  a covariant tensor corresponds in an invariant way with an
a covariant tensor corresponds in an invariant way with an  -linear mapping from the direct product
-linear mapping from the direct product 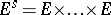 (
( times) into
times) into 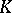 by taking the components of the covariant tensor
by taking the components of the covariant tensor 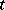 relative to the basis
relative to the basis  as the values of the
as the values of the  -linear mapping
-linear mapping  at the basis vectors
at the basis vectors 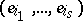 in
in  , and conversely; for this reason a covariant tensor is sometimes defined as a multilinear functional on
, and conversely; for this reason a covariant tensor is sometimes defined as a multilinear functional on 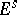 .
.
For references see Covariant vector.
Covariant tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covariant_tensor&oldid=13043