Method of undetermined coefficients in developing numerical algorithms
A special method for constructing algorithms based on the requirement that the algorithms should be exact or have an error of prescribed order of accuracy on some set of problems.
A typical example of problems that can be solved by the method of undetermined coefficients is the following (see [1], [2]). (It can also be solved by other methods.) Let the values  of a function be known. It is required to construct a formula for the approximation of the function
of a function be known. It is required to construct a formula for the approximation of the function
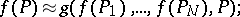 |
to construct a formula for computing the derivative:
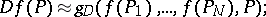 |
and to construct a formula for computing the integral:
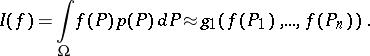 |
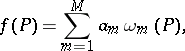
To solve the last of these problems one is given some form of an approximate solution, for example, linear:
 |
and one determines the coefficients 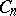 from the requirement that the approximate formula
from the requirement that the approximate formula 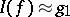 should be exact for functions of a certain collection; for example, for those of the form
should be exact for functions of a certain collection; for example, for those of the form
 |
where the 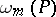 are fixed and the
are fixed and the 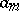 are arbitrary. As a rule one takes
are arbitrary. As a rule one takes 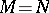 . For the equality
. For the equality
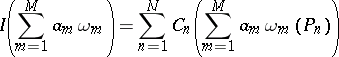 |
to hold for all 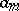 it suffices that
it suffices that
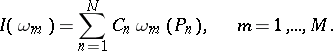 |
From this one determines the  (if this is possible).
(if this is possible).
Sometimes one is given a more complicated form of dependence. For example, frequently it is known that the function in question has a good approximation by functions of the form
 |
where the  are known. The parameters
are known. The parameters 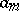 are chosen from the system of equations
are chosen from the system of equations
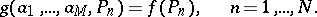 |
In the case of formulas for numerical integration, often the coordinates of the nodes of integration stand out as unknown parameters. For example, in the Gauss quadrature formula
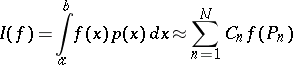 |
one considers as free parameters the coordinates of the nodes 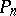 ; owing to this one succeeds in constructing quadratures that are exact for polynomials of degree
; owing to this one succeeds in constructing quadratures that are exact for polynomials of degree 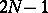 . In the construction of approximations of differential equations by the method of undetermined coefficients it is required that under substitution in a finite-difference scheme the solutions of the problem give compatible (discrepancy) values of prescribed order of smallness in relation to the step of the grid. Such a device lies at the basis of ways for constructing Runge–Kutta methods and finite-difference methods (see [1], [2]).
. In the construction of approximations of differential equations by the method of undetermined coefficients it is required that under substitution in a finite-difference scheme the solutions of the problem give compatible (discrepancy) values of prescribed order of smallness in relation to the step of the grid. Such a device lies at the basis of ways for constructing Runge–Kutta methods and finite-difference methods (see [1], [2]).
The method of undetermined coefficients is also used in constructing approximations of partial differential equations (see [3]).
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [3] | S.K. Godunov, V.S. Ryaben'kii, "The theory of difference schemes" , North-Holland (1964) (Translated from Russian) |
Comments
The techniques of curve and surface fitting may be considered as a form of, what is here called, the method of undetermined coefficients.
Method of undetermined coefficients in developing numerical algorithms. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Method_of_undetermined_coefficients_in_developing_numerical_algorithms&oldid=13040