Correspondence
relation
A generalization of the notion of a binary relation (usually) between two sets or mathematical structures of the same type. Correspondences are widely used in mathematics and also in various applied disciplines, such as theoretical programming, graph theory, systems theory, and mathematical linguistics.
A correspondence between two sets 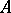 and
and 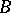 is any subset
is any subset 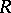 of the Cartesian product
of the Cartesian product 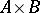 . In other words, a correspondence between
. In other words, a correspondence between 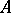 and
and 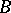 consists of certain ordered pairs
consists of certain ordered pairs 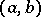 , where
, where  and
and 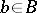 . As a rule, a correspondence is denoted by a triple
. As a rule, a correspondence is denoted by a triple 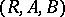 and one may write
and one may write 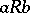 or
or 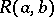 in place of
in place of 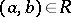 . Instead of "correspondence" the term "binary relation" , or "relation between setsrelation" is sometimes used (in the general case where
. Instead of "correspondence" the term "binary relation" , or "relation between setsrelation" is sometimes used (in the general case where 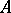 and
and 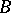 need not coincide).
need not coincide).
For finite sets, the matrix and graphical representations of a correspondence are commonly used. Suppose that 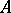 and
and 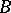 have
have  and
and 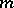 elements, respectively, and let
elements, respectively, and let 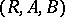 be some correspondence. One can describe this by using an
be some correspondence. One can describe this by using an 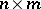 matrix the rows and columns of which are labelled with the elements of
matrix the rows and columns of which are labelled with the elements of 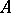 and
and 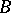 , respectively, and the intersection of the
, respectively, and the intersection of the  -th row with the
-th row with the 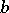 -th column contains 1 if
-th column contains 1 if 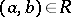 , and
, and  otherwise. Conversely, every
otherwise. Conversely, every 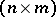 -matrix consisting of zeros and ones describes a unique correspondence between
-matrix consisting of zeros and ones describes a unique correspondence between 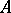 and
and 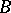 . In the graphical representation, the elements of
. In the graphical representation, the elements of 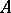 and
and 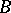 are represented by points in the plane. These points are usually denoted by the same symbols as the corresponding elements. Then
are represented by points in the plane. These points are usually denoted by the same symbols as the corresponding elements. Then  and
and 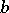 are connected by an arrow (arc) from
are connected by an arrow (arc) from  to
to 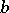 if
if 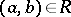 . Thus, the correspondence is represented by an oriented graph.
. Thus, the correspondence is represented by an oriented graph.
The set of all correspondences between two sets 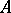 and
and 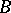 forms a complete Boolean algebra the zero of which is the empty correspondence and the identity of which is the so-called complete correspondence, consisting of all pairs
forms a complete Boolean algebra the zero of which is the empty correspondence and the identity of which is the so-called complete correspondence, consisting of all pairs 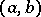 ,
, 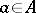 ,
, 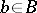 . Let
. Let 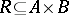 . The set
. The set
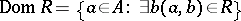 |
is called the domain of definition of 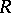 , and the set
, and the set
 |
is called the range, or image, of 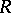 . The correspondence
. The correspondence 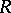 is everywhere defined if
is everywhere defined if 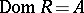 , and surjective if
, and surjective if 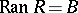 . For every
. For every 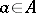 the set
the set
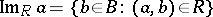 |
is called the image of  with respect to
with respect to 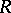 , and for every
, and for every  , the set
, the set
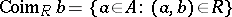 |
is called the co-image (or pre-image) of 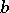 with respect to
with respect to 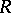 . Then
. Then
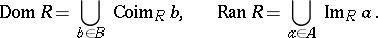 |
Any correspondence 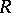 establishes a Galois correspondence between the subsets of
establishes a Galois correspondence between the subsets of 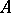 and those of
and those of 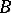 . Namely, to any subset
. Namely, to any subset 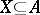 , one assigns the subset
, one assigns the subset  . Together with the dual correspondence
. Together with the dual correspondence 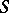 , which assigns to every
, which assigns to every 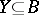 the set
the set 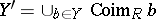 , the Galois correspondence defines a closure operator on both
, the Galois correspondence defines a closure operator on both 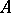 and
and 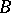 .
.
The inverse or involution 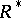 , or
, or 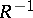 , of a correspondence
, of a correspondence 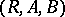 is defined by the equation
is defined by the equation
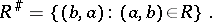 |
This establishes a bijection between the correspondence 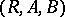 and
and 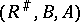 , which is an isomorphism of Boolean algebras. Given two correspondences
, which is an isomorphism of Boolean algebras. Given two correspondences 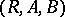 and
and 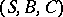 , their product or composite is given by
, their product or composite is given by
 |
Multiplication of correspondences is associative, and its identities are the diagonal binary relations. Moreover,  , and
, and 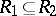 implies that
implies that  . Therefore the correspondences between a family of sets form an ordered category with involution. Multiplication and involution enable one to express the properties of correspondences in terms of algebraic relations. For example, a correspondence
. Therefore the correspondences between a family of sets form an ordered category with involution. Multiplication and involution enable one to express the properties of correspondences in terms of algebraic relations. For example, a correspondence 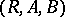 is everywhere defined if
is everywhere defined if 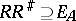 (
(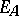 is the diagonal of
is the diagonal of 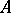 ), and
), and 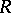 is functional, that is, it is the graph of a function from
is functional, that is, it is the graph of a function from 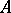 into
into 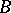 , if
, if 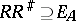 and
and 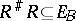 .
.
For any correspondence 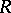 , there are functional correspondences
, there are functional correspondences 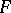 and
and 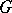 such that
such that 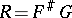 . Moreover,
. Moreover, 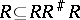 . Any difunctional correspondence induces equivalence relations on the domain and on the image whose quotient sets have the same cardinality. This only holds for difunctional correspondences.
. Any difunctional correspondence induces equivalence relations on the domain and on the image whose quotient sets have the same cardinality. This only holds for difunctional correspondences.
Let 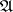 be a class of mathematical structures of the same type that is closed under finite Cartesian products. By a correspondence between two structures
be a class of mathematical structures of the same type that is closed under finite Cartesian products. By a correspondence between two structures 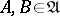 , one means a substructure
, one means a substructure 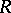 of
of 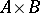 . Thus one has group correspondences, module correspondences, ring correspondences, and others. Such correspondences often have useful descriptions of their structure. For example, let
. Thus one has group correspondences, module correspondences, ring correspondences, and others. Such correspondences often have useful descriptions of their structure. For example, let  and
and 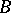 be groups and let
be groups and let 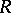 be a subgroup of the direct product
be a subgroup of the direct product 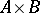 . The sets
. The sets
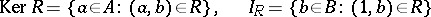 |
are called the kernel and the indeterminacy of 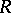 , respectively.
, respectively. 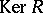 is a normal subgroup of
is a normal subgroup of  ,
, 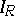 is a normal subgroup of
is a normal subgroup of 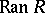 , and the quotient groups
, and the quotient groups 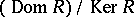 and
and 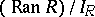 are isomorphic. It follows, in particular that all group correspondences are difunctional.
are isomorphic. It follows, in particular that all group correspondences are difunctional.
References
| [1] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [2] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
| [3] | M.Š. [M.Sh. Tsalenko] Calenko, "Classification of correspondence categories and types of regularities for categories" Trans. Moscow Math. Soc. , 1 (1982) pp. 239–282 Trudy Moskov. Mat. Obshch. , 41 (1980) pp. 241–285 |
Comments
In algebraic geometry correspondences are used widely, [a1], Chapt. 2, 3. They are defined as the following slightly more technical concept. A correspondence 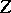 between two (projective) varieties
between two (projective) varieties 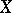 and
and 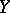 is defined by a closed algebraic subset
is defined by a closed algebraic subset 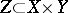 . It is said to be a rational mapping if
. It is said to be a rational mapping if 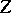 is irreducible and there exists a Zariski-open subset
is irreducible and there exists a Zariski-open subset 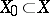 such that each
such that each 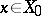 is related by
is related by 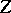 to one and only one point of
to one and only one point of 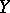 (i.e.
(i.e.  ). The correspondence
). The correspondence 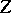 is said to be a birational mapping if both
is said to be a birational mapping if both 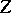 and
and 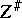 are rational mappings.
are rational mappings.
References
| [a1] | D. Mumford, "Algebraic geometry" , 1. Complex projective varieties , Springer (1976) |
Correspondence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Correspondence&oldid=13039