Modus ponens

law of detachment, rule of detachment

A derivation rule in formal logical systems. The rule of modus ponens is written as a scheme

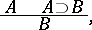where and denote formulas in a formal logical system, and is the logical connective of implication. Modus ponens allows one to deduce from the premise (the minor premise) and (the major premise). If and are true in some interpretation of the formal system, then is true. Modus ponens, together with other derivation rules and axioms of a formal system, determines the class of formulas that are derivable from a set of formulas 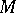as the least class that contains the formulas from and the axioms, and closed with respect to the derivation rules.

Modus ponens can be considered as an operation on the derivations of a given formal system, allowing one to form the derivation of a given formula 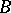from the derivation 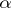of and the derivation of .

Comments

The more precise Latin name of the law of detachment is modus ponendo ponens. In addition there is modus tollendo ponens, which is written as the scheme

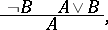where stands for negation and denotes the logical "or" .

References

[a1]	P. Suppes, "Introduction to logic" , v. Nostrand (1957)
[a2]	A. Grzegorczyk, "An outline of mathematical logic" , Reidel (1974)