Chebyshev centre

of a bounded set 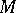in a metric space

An element 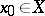for which

(*)

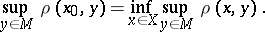The quantity (*) is the Chebyshev radius of the set 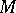. If a normed linear space is dual to some normed linear space, then any bounded set 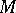has at least one Chebyshev centre. There exists a Banach space and a three-point set in it that has no Chebyshev centre. Every bounded set in a Banach space 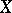has at most one Chebyshev centre if and only if 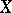is uniformly convex in every direction, that is, if for any 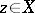and any 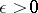there exists a number 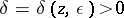such that if 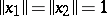, 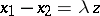and , then . The Chebyshev centre of every bounded set 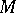in a normed linear space of dimension greater than two is contained in the convex hull of that set if and only if is a Hilbert space. A Chebyshev centre is a special case of the more general notion of a best -lattice.

References

[1]	Itogi Nauki. Mat. Anal. 1967 (1969) pp. 75–132