Integration by parts

One of the methods for calculating integrals. It consists in representing an integral of an expression of the form 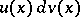by an integral of 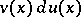. For a definite integral the formula of integration by parts is

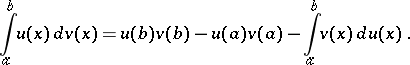(1)

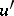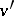It is applicable under the assumptions that , and their derivatives , are continuous on .

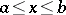The analogue of (1) for an indefinite integral is

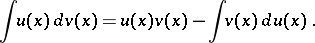(2)

The analogue of (1) for a multiple integral is

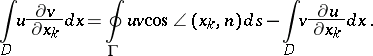(3)

Here 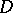is a domain in 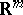with smooth (or at least piecewise-smooth) boundary 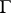; ; 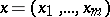and 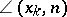is the angle between the 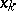-axis and the outward normal to . Formula (3) holds if, e.g., , and their first-order partial derivatives are continuous on 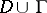. If the integrals in (3) are understood as Lebesgue integrals, then the formula is true if and belong to a Sobolev space: , 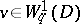for any with .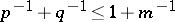

References

[1]	V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian)
[2]	L.D. Kudryavtsev, "Mathematical analysis" , 1–2 , Moscow (1970) (In Russian)
[3]	S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian)

Comments

Formula (1) is valid whenever both and are absolutely continuous (cf. Absolute continuity, 3)) on the closed interval . In this generality the integral must be taken in the Lebesgue sense (cf. Lebesgue integral).

For additional references see also Improper integral.

References

[a1]	E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965)
[a2]	K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981)