Unbiased test
A statistical test of size (level) 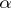 ,
, 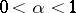 , for testing a compound hypothesis
, for testing a compound hypothesis 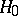 :
: 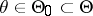 against a compound alternative
against a compound alternative 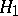 :
: 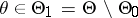 , whose power function
, whose power function  (cf. Power function of a test) satisfies
(cf. Power function of a test) satisfies
 |
 |
In many problems in statistical hypotheses testing there are no uniformly most-powerful tests (cf. Uniformly most-powerful test). But if one restricts the class of tests, then there may be uniformly most-powerful tests in that class. If in the problem of testing the hypothesis 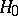 against the alternative
against the alternative 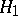 there is a uniformly most-powerful test, then it is unbiased (cf. Unbiased test), since the power of such a test cannot be less than that of the so-called trivial test whose critical function
there is a uniformly most-powerful test, then it is unbiased (cf. Unbiased test), since the power of such a test cannot be less than that of the so-called trivial test whose critical function 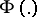 is constant and equal to the size
is constant and equal to the size 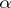 , that is,
, that is,  , where
, where 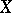 is the random variable whose realization is used to test the hypothesis
is the random variable whose realization is used to test the hypothesis 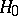 against the alternative
against the alternative 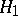 .
.
Example. The sign test is uniformly most-powerful unbiased in the problem of testing the hypothesis 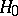 according to which the unknown true value of the parameter
according to which the unknown true value of the parameter 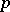 of the binomial distribution is equal to
of the binomial distribution is equal to 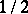 against the alternative
against the alternative 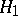 :
: 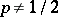 .
.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959) |
Unbiased test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unbiased_test&oldid=12993