Spectral sequence
A sequence of differential modules, each of which is the homology module of the preceding one. One usually studies spectral sequences of bigraded (less often graded or trigraded) modules, which are represented graphically in the form of tables in the plane superimposed on one another. More generally one can study spectral sequences of objects of an arbitrary Abelian category (e.g., bimodules, rings, algebras, co-algebras, Hopf algebras, etc.).
All known spectral sequences can be obtained from exact couples. An exact couple 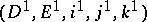 is defined as an exact diagram of the form
is defined as an exact diagram of the form
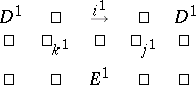 |
The homomorphism 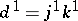 is a differential in
is a differential in 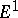 . From any exact couple one can construct the derived exact couple
. From any exact couple one can construct the derived exact couple 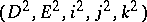 , for which
, for which 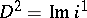 and
and 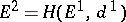 . By iterating this construction one obtains the spectral sequence
. By iterating this construction one obtains the spectral sequence 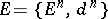 .
.
1) The Leray spectral sequence. A filtered chain complex of modules 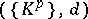 determines an exact couple of bigraded modules
determines an exact couple of bigraded modules 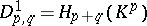 ,
, 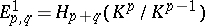 . In the associated spectral sequence, the bidegree of the differential
. In the associated spectral sequence, the bidegree of the differential 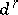 is equal to
is equal to 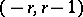 , and
, and
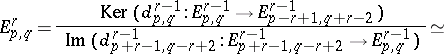 |
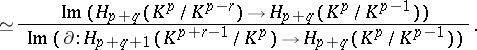 |
The modules 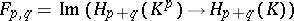 form a filtration of
form a filtration of 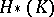 . The bigraded module
. The bigraded module
 |
 |
is called the associated graded module of 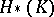 . The filtration
. The filtration 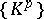 is called regular if
is called regular if 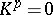 when
when 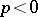 ,
, 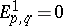 when
when 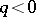 and
and 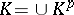 . For a regular filtration,
. For a regular filtration, 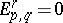 when
when 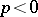 or
or 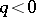 ; such a spectral sequence is called a first-quadrant spectral sequence. Moreover,
; such a spectral sequence is called a first-quadrant spectral sequence. Moreover, 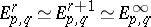 when
when 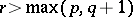 . In this case one says that the spectral sequence converges to
. In this case one says that the spectral sequence converges to 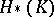 , and writes
, and writes  .
.
2) The Leray–Serre spectral sequence is a special case of the Leray spectral sequence above arising from a chain (or cochain) complex of a filtered topological space. E.g., the filtration of a CW-complex 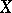 by its skeletons gives the collapsing spectral sequence
by its skeletons gives the collapsing spectral sequence 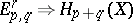 , for which
, for which 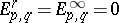 when
when 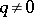 and
and 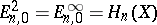 . The Leray–Serre spectral sequence is obtained from the filtration of the total space
. The Leray–Serre spectral sequence is obtained from the filtration of the total space 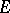 of the Serre fibration
of the Serre fibration 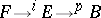 by the pre-images
by the pre-images 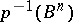 of the skeletons
of the skeletons 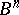 of the base
of the base 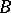 . If the fibre
. If the fibre 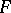 and base
and base 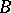 are path-connected, then for every coefficient group
are path-connected, then for every coefficient group 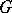 this gives the spectral sequence
this gives the spectral sequence 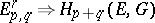 with differentials
with differentials 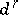 of bidegree
of bidegree 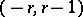 for which
for which
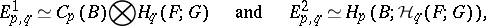 |
where 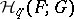 is a system of local coefficients over
is a system of local coefficients over 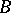 consisting of the groups
consisting of the groups 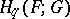 . The homomorphism
. The homomorphism 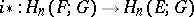 coincides with the composite
coincides with the composite
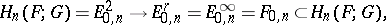 |
and the homomorphism 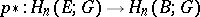 coincides with the composite
coincides with the composite
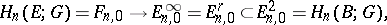 |
where  is sufficiently large. The differential
is sufficiently large. The differential 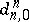 of the spectral sequence coincides with the transgression
of the spectral sequence coincides with the transgression 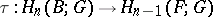 .
.
This homology Leray–Serre spectral sequence is dual to the cohomology Leray–Serre spectral sequence  , with differentials
, with differentials 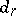 of bidegree
of bidegree 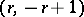 , for which
, for which 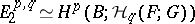 . If
. If  is a ring, then every term
is a ring, then every term 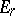 is a bigraded ring,
is a bigraded ring, 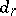 is differentiation in
is differentiation in 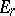 , and the multiplication in
, and the multiplication in 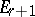 is induced by that in
is induced by that in 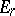 . If
. If 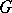 is a field and the base
is a field and the base 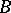 is simply connected, then
is simply connected, then 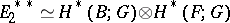 .
.
3) The Atiyah–Hirzebruch (–Whitehead) spectral sequence is obtained by applying the generalized (co)homology functor 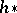 (
(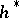 ) to the same filtration of the space
) to the same filtration of the space 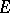 . In its cohomological version,
. In its cohomological version,  ,
, 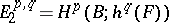 . In contrast to the Leray–Serre spectral sequence, the Atiyah–Hirzebruch spectral sequence for the trivial fibration
. In contrast to the Leray–Serre spectral sequence, the Atiyah–Hirzebruch spectral sequence for the trivial fibration 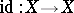 is in general non-collapsing.
is in general non-collapsing.
4) An Eilenberg–Moore spectral sequence is associated with any square of fibrations
 |
In its cohomological version,
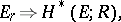 |
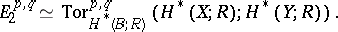 |
If  is a field and the square consists of
is a field and the square consists of 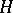 -spaces and
-spaces and 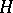 -mappings, then this is a spectral sequence in the category of bigraded Hopf algebras.
-mappings, then this is a spectral sequence in the category of bigraded Hopf algebras.
5) The Adams spectral sequence 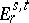 is defined for every prime
is defined for every prime 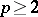 and all spaces
and all spaces 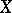 and
and 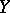 (satisfying certain finiteness conditions). One has
(satisfying certain finiteness conditions). One has
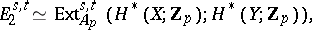 |
where 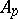 is the Steenrod algebra modulo
is the Steenrod algebra modulo 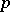 . The bidegree of
. The bidegree of 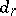 is equal to
is equal to 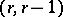 . This spectral sequence converges in the sense that, when
. This spectral sequence converges in the sense that, when 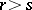 , there is a monomorphism
, there is a monomorphism 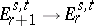 , and so the group
, and so the group  is defined. There is a decreasing filtration
is defined. There is a decreasing filtration 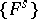 of the group
of the group 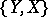 of stable homotopy classes of mappings
of stable homotopy classes of mappings 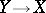 such that
such that
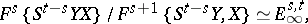 |
and 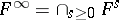 consists of all elements of
consists of all elements of 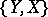 of finite order prime with
of finite order prime with 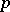 . When
. When 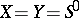 , this spectral sequence enables one "in principle" to calculate the
, this spectral sequence enables one "in principle" to calculate the 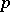 -components of the stable homotopy groups of spheres. The Adams spectral sequence has been generalized by A.S. Mishchenko and S.P. Novikov to arbitrary generalized cohomology theories. There are also extensions of the Adams spectral sequence that converge to non-stable homotopy groups.
-components of the stable homotopy groups of spheres. The Adams spectral sequence has been generalized by A.S. Mishchenko and S.P. Novikov to arbitrary generalized cohomology theories. There are also extensions of the Adams spectral sequence that converge to non-stable homotopy groups.
References
| [1] | R.E. Mosher, M.C. Tangora, "Cohomology operations and applications in homotopy theory" , Harper & Row (1968) |
| [2] | D.B. Fuks, A.T. Fomenko, V.L. Gutenmakher, "Homotopic topology" , Moscow (1969) (In Russian) |
| [3] | J.-P. Serre, "Homologie singulière des espaces fibrés. Applications" Ann. of Math. , 54 (1951) pp. 425–505 |
| [4] | S. MacLane, "Homology" , Springer (1963) |
| [5] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [6] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [7] | S.-T. Hu, "Homotopy theory" , Acad. Press (1959) |
| [8] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958) |
| [9] | S.P. Novikov, "The methods of algebraic topology from the viewpoint of cobordism theory" Math. USSR Izv. , 31 (1967) pp. 827–913 Izv. Akad. Nauk. SSSR Ser. Mat. , 31 (1967) pp. 855–951 |
| [10] | J.F. Adams, "Stable homotopy and generalised homology" , Univ. Chicago Press (1974) |
| [11] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) |
| [12] | L. Smith, "Lectures on the Eilenberg–Moore spectral sequence" , Lect. notes in math. , 134 , Springer (1970) |
| [13] | D.C. Ravenel, "A novices guide to the Adams–Novikov spectral sequence" , Geometric Applications of Homotopy Theory , 2 , Springer (1978) pp. 404–475 |
Comments
Let 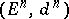 ,
, 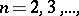 be a spectral sequence, so that
be a spectral sequence, so that 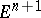 is the homology of
is the homology of 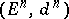 . A spectral sequence defines a series of modules of the initial term
. A spectral sequence defines a series of modules of the initial term 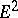 , defined inductively as follows:
, defined inductively as follows:
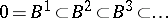 |
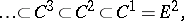 |
with 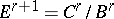 , and
, and 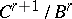 is the kernel of
is the kernel of 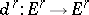 , while
, while 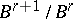 is the image of
is the image of 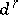 . One now defines the infinity terms:
. One now defines the infinity terms:
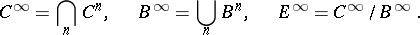 |
The terms 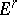 are thought of as successive approximations of
are thought of as successive approximations of 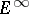 . If
. If 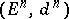 is a spectral sequence of bigraded modules
is a spectral sequence of bigraded modules 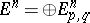 ,
,  , all the
, all the 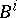 ,
, 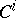 ,
, 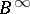 ,
, 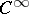 ,
, 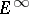 also carry corresponding natural bigraded structures.
also carry corresponding natural bigraded structures.
Sometimes there is an initial term 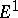 , and then the same construction is carried out with
, and then the same construction is carried out with 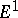 instead of
instead of 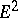 .
.
For a first-quadrant spectral sequence, i.e. 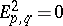 for
for 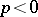 or
or 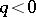 , for given
, for given 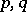 and large enough
and large enough  one has that in
one has that in
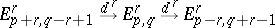 |
both the outside modules are zero, so that 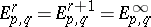 for
for  large enough.
large enough.
For a first-quadrant spectral sequence one also always has that 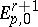 is a submodule of
is a submodule of 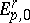 , and
, and 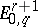 is a quotient of
is a quotient of 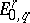 , giving rise to sequences of monomorphisms and epimorphisms:
, giving rise to sequences of monomorphisms and epimorphisms:
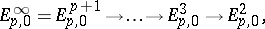 |
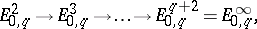 |
which are known as the edge homomorphisms.
Let 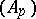 be a filtration of a module
be a filtration of a module 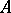 by submodules
by submodules
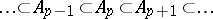 |
with associated graded module 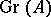 :
:
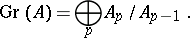 |
A spectral sequence 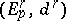 is said to converge to a graded module
is said to converge to a graded module 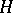 , in symbols
, in symbols
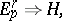 |
if there is a filtration 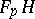 of
of 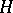 such that
such that
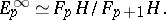 | (*) |
In the usual cases the 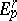 and
and 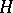 are graded, and then both the filtration and the isomorphism (*) are to be compatible with the grading.
are graded, and then both the filtration and the isomorphism (*) are to be compatible with the grading.
Spectral sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_sequence&oldid=12982