Ricci curvature
of a Riemannian manifold  at a point
at a point 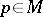
A number corresponding to each one-dimensional subspace of the tangent space  by the formula
by the formula
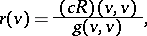 |
where  is the Ricci tensor,
is the Ricci tensor,  is a vector generating the one-dimensional subspace and
is a vector generating the one-dimensional subspace and  is the metric tensor of the Riemannian manifold
is the metric tensor of the Riemannian manifold  . The Ricci curvature can be expressed in terms of the sectional curvatures of
. The Ricci curvature can be expressed in terms of the sectional curvatures of  . Let
. Let  be the sectional curvature at the point
be the sectional curvature at the point 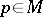 in the direction of the surface element defined by the vectors
in the direction of the surface element defined by the vectors 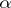 and
and 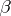 , let
, let 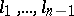 be normalized vectors orthogonal to each other and to the vector
be normalized vectors orthogonal to each other and to the vector  , and let
, and let  be the dimension of
be the dimension of 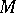 ; then
; then
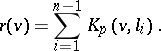 |
For manifolds 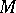 of dimension greater than two the following proposition is valid: If the Ricci curvature at a point
of dimension greater than two the following proposition is valid: If the Ricci curvature at a point  has one and the same value
has one and the same value  in all directions
in all directions  , then the Ricci curvature has one and the same value
, then the Ricci curvature has one and the same value  at all points of the manifold. Manifolds of constant Ricci curvature are called Einstein spaces. The Ricci tensor of an Einstein space is of the form
at all points of the manifold. Manifolds of constant Ricci curvature are called Einstein spaces. The Ricci tensor of an Einstein space is of the form 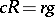 , where
, where  is the Ricci curvature. For an Einstein space the following equality holds:
is the Ricci curvature. For an Einstein space the following equality holds:
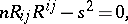 |
where  ,
, 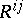 are the covariant and contravariant components of the Ricci tensor,
are the covariant and contravariant components of the Ricci tensor,  is the dimension of the space and
is the dimension of the space and  is the scalar curvature of the space.
is the scalar curvature of the space.
The Ricci curvature can be defined by similar formulas also on pseudo-Riemannian manifolds; in this case the vector is assumed to be anisotropic.
From the Ricci curvature the Ricci tensor can be recovered uniquely:
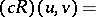 |
 |
References
| [1] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [2] | A.Z. Petrov, "Einstein spaces" , Pergamon (1969) (Translated from Russian) |
Comments
References
| [a1] | N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) |
| [a2] | A.L. Besse, "Einstein manifolds" , Springer (1987) |
Ricci curvature. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ricci_curvature&oldid=12970