Star of a function element
Mittag-Leffler star
A star-like domain in which the given element
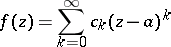 |
of an analytic function (cf. Analytic function, element of an) can be continued analytically along rays issuing from the centre  . The star consists of those points of the complex
. The star consists of those points of the complex  -plane which can be reached by analytic continuation of
-plane which can be reached by analytic continuation of  as a power series along all possible rays from the centre
as a power series along all possible rays from the centre  of the series. If
of the series. If  ,
,  , is a ray on which there are points that cannot be reached this way, then there is a point
, is a ray on which there are points that cannot be reached this way, then there is a point  on the ray such that the element can be continued to any point of the interval
on the ray such that the element can be continued to any point of the interval  but not beyond. If continuation is possible to any point of the ray, one puts
but not beyond. If continuation is possible to any point of the ray, one puts 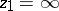 . The set of points belonging to all intervals
. The set of points belonging to all intervals 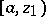 is a (simply-connected) star-like domain about
is a (simply-connected) star-like domain about  , called the star of the function element and denoted by
, called the star of the function element and denoted by  . Analytic continuation in
. Analytic continuation in  results in a regular analytic function
results in a regular analytic function  , which is the univalent branch in
, which is the univalent branch in 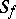 of the complete analytic function generated by the given element.
of the complete analytic function generated by the given element.
All points of the boundary  are accessible (cf. Attainable boundary point). In questions of analytic continuation (see also Hadamard theorem) one also defines angular, attainable and well-attainable points of
are accessible (cf. Attainable boundary point). In questions of analytic continuation (see also Hadamard theorem) one also defines angular, attainable and well-attainable points of  . A point
. A point 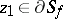 is called an angular boundary point of the star of a function element if its modulus
is called an angular boundary point of the star of a function element if its modulus  is minimal among all points of
is minimal among all points of 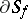 with the same argument
with the same argument 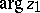 . A point
. A point  is called an attainable boundary point of the star if there is a half-disc
is called an attainable boundary point of the star if there is a half-disc  such that
such that 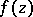 is regular everywhere inside
is regular everywhere inside 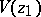 and at the points of its diameter other than
and at the points of its diameter other than 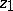 . The point is said to be well-attainable if there is a sector
. The point is said to be well-attainable if there is a sector 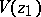 with apex
with apex 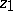 and angle greater than
and angle greater than  , such that
, such that 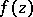 is regular in the domain
is regular in the domain  for sufficiently small
for sufficiently small 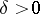 .
.
G. Mittag-Leffler
showed that a regular function 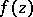 can be expressed in its star as a series of polynomials convergent inside
can be expressed in its star as a series of polynomials convergent inside 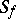 :
:
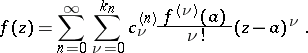 | (*) |
Formula (*) is known as the Mittag-Leffler expansion in a star. The degrees of the polynomials 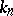 and their coefficients
and their coefficients  ,
, 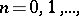 are independent of the form of
are independent of the form of 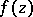 and can be evaluated once and for all. This was done by P. Painlevé (see [2], [3]).
and can be evaluated once and for all. This was done by P. Painlevé (see [2], [3]).
References
| [1a] | G. Mittag-Leffler, "Sur la répresentation analytique d'une branche uniforme d'une fonction monogène I" Acta Math. , 23 (1899) pp. 43–62 |
| [1b] | G. Mittag-Leffler, "Sur la répresentation analytique d'une branche uniforme d'une fonction monogène II" Acta Math. , 24 (1901) pp. 183–204 |
| [1c] | G. Mittag-Leffler, "Sur la répresentation analytique d'une branche uniforme d'une fonction monogène III" Acta Math. , 24 (1901) pp. 205–244 |
| [1d] | G. Mittag-Leffler, "Sur la répresentation analytique d'une branche uniforme d'une fonction monogène IV" Acta Math. , 26 (1902) pp. 353–393 |
| [1e] | G. Mittag-Leffler, "Sur la répresentation analytique d'une branche uniforme d'une fonction monogène V" Acta Math. , 29 (1905) pp. 101–182 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian) |
| [3] | E. Borel, "Leçons sur les fonctions de variables réelles et les développements en séries de polynômes" , Gauthier-Villars (1905) |
Star of a function element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Star_of_a_function_element&oldid=12951