Cohomology

A term used with respect to functors of a homological nature that, in contrast to homology, depend contravariantly, as a rule, on the objects of the basic category on which they are defined. In contrast to homology, connecting homomorphisms in exact cohomology sequences raise the dimension. In typical situations, cohomology occurs simultaneously with the corresponding homology.

E.G. Sklyarenko

Cohomology of a topological space.

This is a graded group

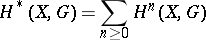associated with a topological space 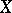and an Abelian group 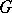. The notion of cohomology is dual to that of homology (see Homology theory; Homology group; Aleksandrov–Čech homology and cohomology). If 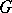is a ring, then a natural product is defined in the group 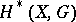(Kolmogorov–Alexander product or 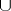-product), converting this group into a graded ring (cohomology ring). In the case when 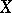is a differentiable manifold, the cohomology ring 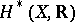can be calculated by means of differential forms on 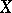(see de Rham theorem).

Cohomology with values in a sheaf of Abelian groups.

This is a generalization of ordinary cohomology of a topological space. There are two cohomology theories with values (or coefficients) in sheaves of Abelian groups: Čech cohomology and Grothendieck cohomology.

Čech cohomology. Let 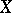be a topological space, 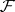a sheaf of Abelian groups on 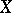and an 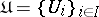open covering of 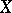. Then by an 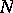-dimensional cochain of 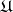one means a mapping 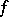that associates with each ordered set 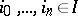such that

a section 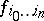of the sheaf 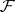over 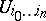. The set of all -dimensional cochains, 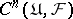, is an Abelian group (with respect to addition). The coboundary operator

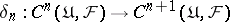is defined as follows:

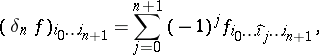where the symbol denotes that the corresponding index should be omitted.

The sequence

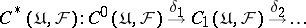is a complex (the Čech complex). The cohomology of this complex is denoted by 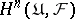and is called the Čech cohomology of the covering with values in . The group 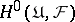is the same as the group 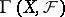of sections of 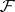. In calculating the cohomology, the Čech complex can be replaced by its subcomplex consisting of the alternating cochains, that is, cochains that change sign on permutation of two indices and are equal to when two indices are equal.

If the covering 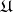is a refinement of 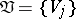, that is, for each 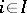there exists a 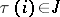such that 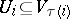, then a canonical homomorphism 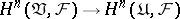is defined which does not depend on the refinement . The -dimensional Čech cohomology group of the space 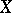with values in 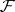is now defined by the formula:

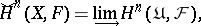where the inductive limit is taken over the directed (with respect to refinement) set of equivalence classes of open coverings (two coverings being equivalent if and only if each is a refinement of the other). The definition of Čech cohomology is also applicable to pre-sheaves.

A disadvantage of Čech cohomology is that (for non-paracompact spaces) it does not form a cohomology functor (see Homology functor). In the case when is the constant sheaf corresponding to the Abelian group 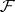, the groups 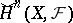are the same as the Aleksandrov–Čech cohomology groups with coefficients in the group .

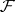Grothendieck cohomology. One considers the functor 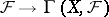from the category of sheaves of Abelian groups on 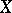to the category of Abelian groups. The right derived functors (cf. Derived functor) of this functor are called the -dimensional Grothendieck cohomology groups with values in the sheaf 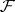and are denoted by 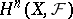, 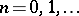. Corresponding to an exact sequence of sheaves of Abelian groups

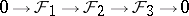there is an exact sequence

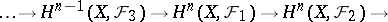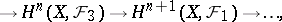that is, 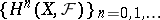forms a cohomology functor. Furthermore, 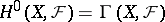. If 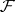is a flabby sheaf, 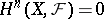(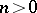). These three properties of Grothendieck cohomology characterize the functor 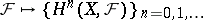uniquely up to an isomorphism.

For the calculation of the Grothendieck cohomology of the sheaf 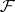one can use the left resolution of 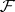consisting of sheaves the Grothendieck cohomology of which vanishes in positive dimensions. For example, on arbitrary topological spaces one can take the resolution by flabby sheaves, and on paracompact spaces, the resolution by the soft or fine sheaves (cf. Fine sheaf; Soft sheaf).

Grothendieck cohomology is related to cohomology of coverings in the following way. Let 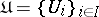be an open covering of the space 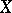. Then there exists a spectral sequence 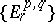converging to 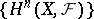and such that

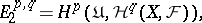where 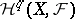is the pre-sheaf associating the group 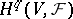with the open set 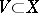. If the cohomology of all 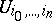with values in 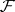vanishes in positive dimensions, then the sequence is degenerate and

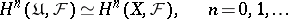(Leray's theorem). In the general case the spectral sequence defines a functorial homomorphism

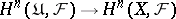and, on passing to the limit, a functorial homomorphism

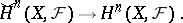The latter homomorphism is bijective for 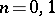, injective (but not, in general, surjective) for 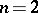and, when is paracompact, bijective for all . Thus, for a paracompact space ,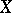

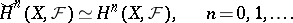A generalization of the cohomology groups defined above are the cohomology groups 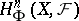with supports in a family . A family 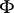of closed subsets of 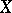is called a family of supports if: 1) any closed subset of a member of 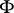belongs to 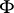; and 2) the union of any two members of 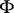is in 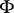. The groups 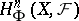are defined as the right derived functors of the functor 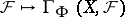, where 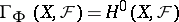is the group of sections of the sheaf with supports in . 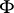They form a cohomology functor. If 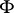is the family of all closed sets, then . Another important special case: 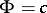, the family of all compact subsets. The groups 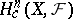are called the cohomology groups with compact supports.

In the case when 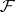is a sheaf of rings, the group

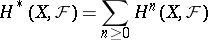has a naturally defined multiplication, converting it into a graded ring (a cohomology ring). Here, associativity in the sheaf 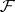implies associativity of multiplication in 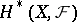, while a sheaf of commutative rings or Lie rings gives rise to a graded commutative or Lie cohomology ring, respectively. If 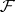is a sheaf of modules over a sheaf of rings 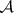, then the are modules over the ring .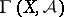

Concerning cohomology with values in a sheaf of non-Abelian groups see Non-Abelian cohomology.

References

[1]	A. Grothendieck, "Sur quelques points d'algèbre homologique" Tôhoku Math. J. , 9 (1957) pp. 119–221
[2]	R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958)
[3]	J.-P. Serre, "Faiseaux algébriques cohérentes" Ann. of Math. (2) , 61 : 2 (1955) pp. 197–278

D.A. Ponomarev

Comments

See Singular homology for a description of singular homology.

References

[a1]	J.-P. Serre, "Homologie singulière des espaces fibrés. Applications" Ann. of Math. , 54 (1951) pp. 425–505
[a2]	N.E. Steenrod, S. Eilenberg, "Foundations of algebraic topology" , Princeton Univ. Press (1966)
[a3]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapts. 4; 5
[a4]	A. Dold, "Lectures on algebraic topology" , Springer (1980)

Cohomology of spaces with operators.

Cohomological invariants of a topological space with a group action defined on it. Let 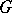be a group acting on the space 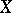, where for each 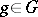the mapping 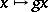is a homeomorphism 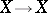. Then by a 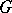-sheaf of Abelian groups on 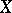one means a sheaf of Abelian groups on 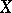together with an action of the group 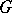which is continuous, compatible with the action on 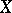and which maps stalks of the sheaf isomorphically onto one another. A natural 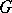-module structure is defined on the group of sections of a 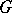-sheaf 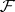(and more generally on the cohomology groups 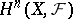). The 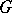-sheaves of Abelian groups on form an Abelian category, each object of which admits an imbedding into an injective object. The functor 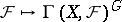from this category into the category of Abelian groups, where 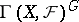is the group of 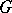-invariant sections of the 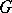-sheaf 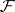, has right derived functors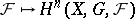 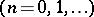, where 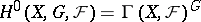, which constitute a cohomology functor. The groups 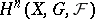play a fundamental role in the study of the connection between the cohomology of the space 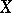, the quotient space 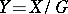and the group 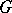. There exists a spectral sequence 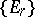with second term 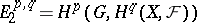and converging to 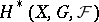. Let 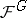be the sheaf of invariants of the direct image 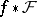( 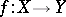being the natural projection) regarded as a 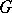-sheaf on the space 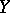on which 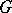acts trivially. If 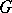acts properly discontinuously and freely on 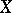(see Discrete group of transformations), then 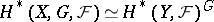(see [1]). In particular, if 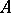is a 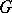-module, then the constant sheaf 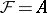on 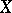has a natural 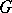-sheaf structure and the sheaf 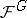is locally constant on 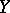. In this case the spectral sequence 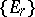satisfies the condition 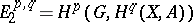and converges to 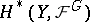(spectral sequence of a covering). 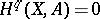If, moreover, is connected and for 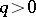, then 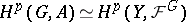, which gives a topological interpretation of the cohomology of the group 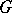[2]. If 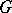is properly discontinuous and 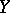is paracompact, then the groups can be calculated in the same way as Čech cohomology, by means of 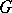-invariant coverings of 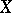(see [1]).

In the case when 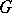is a Lie group acting freely and differentiably on a differentiable manifold 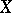, where 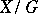is a differentiable manifold, the analogue 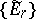of the spectral sequence of the covering is well-known [3]. The sequence 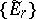converges to the cohomology of the complex of 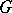-invariant differential forms on 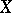and 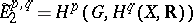, where the cohomology of 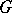is calculated by means of cochains of class .

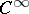See also Cohomology of groups; Equivariant cohomology.

References

[1]	A. Grothendieck, "Sur quelques points d'algèbre homologique" Tôhoku Math. J. , 9 (1957) pp. 119–221
[2]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)
[3]	W.T. van Est, "A generalization of the Cartan–Leray spectral sequence I, II" Proc. Nederl. Akad. Wetensch. Ser. A , 61 (1958) pp. 399–413

A.L. OnishchikD.A. Ponomarev