Absorption laws
From Encyclopedia of Mathematics
Identities of the form
 |
where  and
and  are two-place operations on some set
are two-place operations on some set 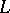 . If these operations satisfy also the laws of commutativity and associativity, then the relation
. If these operations satisfy also the laws of commutativity and associativity, then the relation  defined by the equivalence
defined by the equivalence
 | (*) |
(or equivalently, by the equivalence  ) is an order relation for which
) is an order relation for which 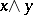 is the infimum of the elements
is the infimum of the elements  and
and  , while
, while  is the supremum. On the other hand, if the ordered set
is the supremum. On the other hand, if the ordered set  contains an infimum
contains an infimum 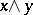 and a supremum
and a supremum 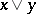 for any pair of elements
for any pair of elements  and
and  , then for the operations
, then for the operations  and
and  the laws of absorption, commutativity and associativity, as well as the equivalence (*) apply.
the laws of absorption, commutativity and associativity, as well as the equivalence (*) apply.
References
| [1] | E. Rasiowa, R. Sikorski, "The mathematics of metamathematics" , Polska Akad. Nauk (1963) |
Comments
Instead of absorption laws one also uses the term absorptive laws, cf. [a1], Chapt. 2, Sect. 4.
References
| [a1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
How to Cite This Entry:
Absorption laws. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absorption_laws&oldid=12933
Absorption laws. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absorption_laws&oldid=12933
This article was adapted from an original article by V.N. Grishin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article