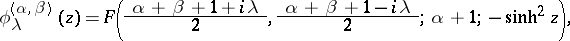A solution of a hypergeometric equation
 | (1) |
A hypergeometric function can be defined with the aid of the so-called Gauss series
 | (2) |
where 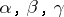 are parameters which assume arbitrary real or complex values except for
are parameters which assume arbitrary real or complex values except for 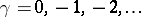 ;
;  is a complex variable; and
is a complex variable; and 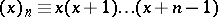 . The function
. The function 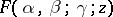 is called a hypergeometric function of the first kind. The second linearly independent solution of (1),
is called a hypergeometric function of the first kind. The second linearly independent solution of (1),
is called a hypergeometric function of the second kind.
The series (2) is absolutely and uniformly convergent if 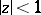 ; the convergence also extends over the unit circle if
; the convergence also extends over the unit circle if 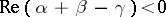 ; if
; if 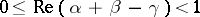 it converges at all points of the unit circle except
it converges at all points of the unit circle except 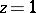 . However, there exists an analytic continuation of the hypergeometric function (2) to the exterior
. However, there exists an analytic continuation of the hypergeometric function (2) to the exterior 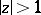 of the unit disc with the slit
of the unit disc with the slit 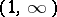 [1]. The function
[1]. The function 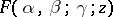 is a univalent analytic function in the complex
is a univalent analytic function in the complex  -plane with slit
-plane with slit  . If
. If  or
or 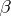 are zero or negative integers, the series (2) terminates after a finite number of terms, and the hypergeometric function is a polynomial in
are zero or negative integers, the series (2) terminates after a finite number of terms, and the hypergeometric function is a polynomial in  .
.
If 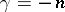 ,
, 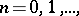 the hypergeometric function is not defined, but
the hypergeometric function is not defined, but
Elementary relations. The six functions
are said to be contiguous to the hypergeometric function 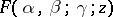 . There exists a linear relationship between that function and any two functions which are contiguous to it. For instance, C.F. Gauss [2], [3] was the first to find 15 formulas of the type
. There exists a linear relationship between that function and any two functions which are contiguous to it. For instance, C.F. Gauss [2], [3] was the first to find 15 formulas of the type
The associated functions 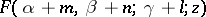 , where
, where 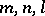 are integers, can be obtained by iterated application of Gauss' relations. The following differentiation formulas apply:
are integers, can be obtained by iterated application of Gauss' relations. The following differentiation formulas apply:
Equation (1) has 24 solutions of the form
where 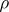 ,
, 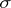 ,
, 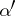 ,
, 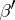 , and
, and 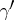 are linear functions of
are linear functions of 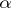 ,
, 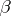 and
and 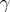 ; and
; and  and
and 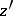 are connected by a bilinear transformation. Any three solutions are linearly dependent [2]. There exist square, cubic and higher-order transformations [2]–[5].
are connected by a bilinear transformation. Any three solutions are linearly dependent [2]. There exist square, cubic and higher-order transformations [2]–[5].
Principal integral representations. If 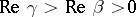 and
and 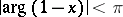 , Euler's formula
, Euler's formula
 | (3) |
holds. By expanding 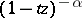 into a binomial series and using contour integrals for the beta-function, other integral representations can be obtained [2]. The integral (3) and other similar formulas defining an analytic function of
into a binomial series and using contour integrals for the beta-function, other integral representations can be obtained [2]. The integral (3) and other similar formulas defining an analytic function of  which is single-valued throughout the
which is single-valued throughout the  -plane can also be used as analytic continuations of
-plane can also be used as analytic continuations of 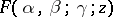 into the domain
into the domain 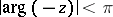 . Other analytic continuations also exist [1], [2].
. Other analytic continuations also exist [1], [2].
The asymptotic behaviour of hypergeometric functions for large values of 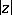 is completely described by formulas yielding analytic continuations in a neighbourhood of the point
is completely described by formulas yielding analytic continuations in a neighbourhood of the point 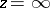 [1], [2], [3]. If
[1], [2], [3]. If 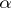 ,
, 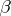 and
and  are given and
are given and 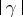 is sufficiently large,
is sufficiently large,  ,
, 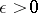 , then, if
, then, if 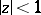 :
:
A similar expression is obtained for 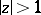 .
.
For fixed 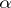 ,
, 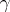 and
and  ,
, 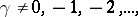
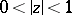 , and
, and 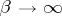 ,
, 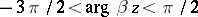 ,
,
See also [2], [5], [6].
Representation of functions by hypergeometric functions. The elementary functions:
The complete elliptic integrals of the first and second kinds (cf. Elliptic integral):
The adjoint Legendre functions:
The Chebyshev polynomials:
The Legendre polynomials:
The ultraspherical polynomials:
The Jacobi polynomials:
Generalizations of hypergeometric functions. The generalized hypergeometric function
is said to be the solution of the hypergeometric equation of order 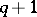 [2]. There are also other generalizations of hypergeometric functions, such as generalizations to include the case of several variables [2].
[2]. There are also other generalizations of hypergeometric functions, such as generalizations to include the case of several variables [2].
References
| [1] | N.N. Lebedev, "Special functions and their applications" , Prentice-Hall (1965) (Translated from Russian) |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
| [3] | I.S. Gradshtein, I.M. Ryzhik, "Table of integrals, series and products" , Acad. Press (1980) (Translated from Russian) |
| [4] | E.E. Kummer, "Ueber die hypergeometrische Reihe 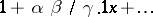 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 |
| [5] | A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970) |
| [6] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) |
| [7] | A.L. Lebedev, R.M. Fedorova, "Handbook of mathematical tables" , Moscow (1956) (In Russian) |
| [8] | N.M. Burunova, "Handbook of mathematical tables" , Moscow (1959) (In Russian) (Supplement I) |
| [9] | A.A. Fletcher, J.C.P. Miller, L. Rosenhead, L.J. Comrie, "An index of mathematical tables" , 1–2 , Oxford Univ. Press (1962) |
To the list of functions representable by hypergeometric functions the Jacobi functions should be added:
cf. [a2].
An important generalization is given by the basic hypergeometric functions, cf. [a1].
References
| [a1] | G. Gasper, M. Rahman, "Basic hypergeometric series" , Cambridge Univ. Press (1989) |
| [a2] | T.H. Koornwinder, "Jacobi functions and analysis on noncompact semisimple Lie groups" R.A. Askey (ed.) T.H. Koornwinder (ed.) W. Schempp (ed.) , Special functions: group theoretical aspects and applications , Reidel (1984) pp. 1–85 |


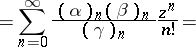
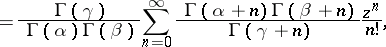
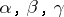 are parameters which assume arbitrary real or complex values except for
are parameters which assume arbitrary real or complex values except for 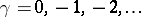 ;
;  is a complex variable; and
is a complex variable; and 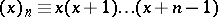 . The function
. The function 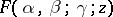 is called a hypergeometric function of the first kind. The second linearly independent solution of (1),
is called a hypergeometric function of the first kind. The second linearly independent solution of (1),
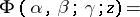
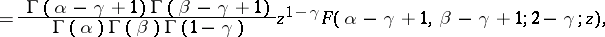
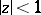 ; the convergence also extends over the unit circle if
; the convergence also extends over the unit circle if 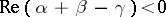 ; if
; if 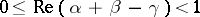 it converges at all points of the unit circle except
it converges at all points of the unit circle except 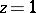 . However, there exists an analytic continuation of the hypergeometric function (2) to the exterior
. However, there exists an analytic continuation of the hypergeometric function (2) to the exterior 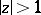 of the unit disc with the slit
of the unit disc with the slit 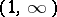 [1]. The function
[1]. The function 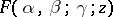 is a univalent analytic function in the complex
is a univalent analytic function in the complex  -plane with slit
-plane with slit  . If
. If  or
or 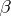 are zero or negative integers, the series (2) terminates after a finite number of terms, and the hypergeometric function is a polynomial in
are zero or negative integers, the series (2) terminates after a finite number of terms, and the hypergeometric function is a polynomial in  .
.
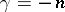 ,
, 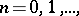 the hypergeometric function is not defined, but
the hypergeometric function is not defined, but
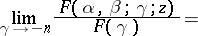
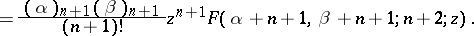
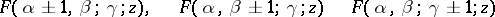
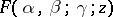 . There exists a linear relationship between that function and any two functions which are contiguous to it. For instance, C.F. Gauss [2], [3] was the first to find 15 formulas of the type
. There exists a linear relationship between that function and any two functions which are contiguous to it. For instance, C.F. Gauss [2], [3] was the first to find 15 formulas of the type
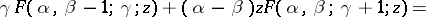

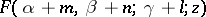 , where
, where 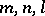 are integers, can be obtained by iterated application of Gauss' relations. The following differentiation formulas apply:
are integers, can be obtained by iterated application of Gauss' relations. The following differentiation formulas apply:
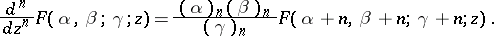
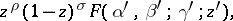
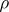 ,
, 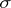 ,
, 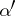 ,
, 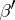 , and
, and 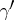 are linear functions of
are linear functions of 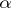 ,
, 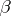 and
and 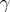 ; and
; and  and
and 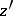 are connected by a bilinear transformation. Any three solutions are linearly dependent [2]. There exist square, cubic and higher-order transformations [2]–[5].
are connected by a bilinear transformation. Any three solutions are linearly dependent [2]. There exist square, cubic and higher-order transformations [2]–[5].
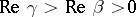 and
and 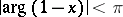 , Euler's formula
, Euler's formula

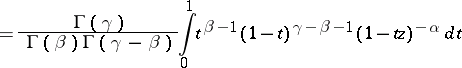
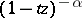 into a binomial series and using contour integrals for the beta-function, other integral representations can be obtained [2]. The integral (3) and other similar formulas defining an analytic function of
into a binomial series and using contour integrals for the beta-function, other integral representations can be obtained [2]. The integral (3) and other similar formulas defining an analytic function of  which is single-valued throughout the
which is single-valued throughout the  -plane can also be used as analytic continuations of
-plane can also be used as analytic continuations of 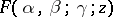 into the domain
into the domain 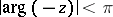 . Other analytic continuations also exist [1], [2].
. Other analytic continuations also exist [1], [2].
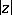 is completely described by formulas yielding analytic continuations in a neighbourhood of the point
is completely described by formulas yielding analytic continuations in a neighbourhood of the point 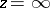 [1], [2], [3]. If
[1], [2], [3]. If 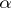 ,
, 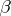 and
and  are given and
are given and 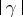 is sufficiently large,
is sufficiently large,  ,
, 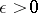 , then, if
, then, if 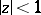 :
:
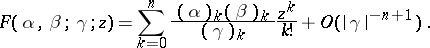
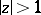 .
.
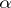 ,
, 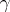 and
and  ,
, 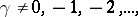
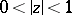 , and
, and 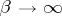 ,
, 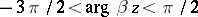 ,
,
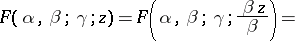
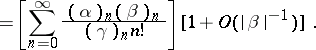
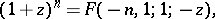
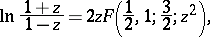

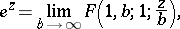
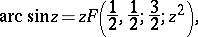
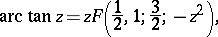
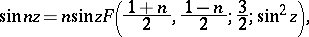
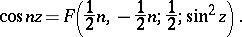
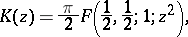
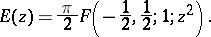
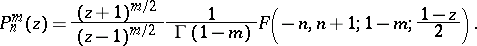
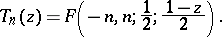
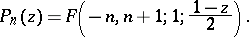
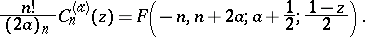
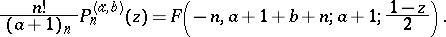
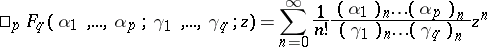
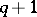 [2]. There are also other generalizations of hypergeometric functions, such as generalizations to include the case of several variables [2].
[2]. There are also other generalizations of hypergeometric functions, such as generalizations to include the case of several variables [2].
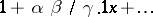 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172
" J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172