Site
topologized category.
A category equipped with a Grothendieck topology, that is, with a structure of "coverings" which makes it possible to define the notion of a sheaf on the category. The motivating example has as underlying category the lattice 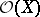 of open sets of a topological space
of open sets of a topological space 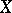 , regarded as a category whose objects are the open sets and whose morphisms are the inclusion mappings between them. A pre-sheaf (of sets) on
, regarded as a category whose objects are the open sets and whose morphisms are the inclusion mappings between them. A pre-sheaf (of sets) on 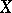 is then just a functor from
is then just a functor from 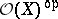 to the category
to the category 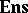 of sets; a pre-sheaf
of sets; a pre-sheaf 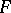 is a sheaf if, for any covering of an open set
is a sheaf if, for any covering of an open set 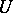 by smaller open sets
by smaller open sets 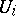 (
(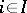 ), the diagram
), the diagram
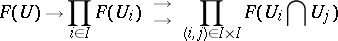 |
(where the arrows are induced in the obvious way by restriction mappings, i.e. by the action of 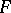 on morphisms of
on morphisms of 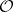 ) is an equalizer. (In more elementary terms, this says that elements of
) is an equalizer. (In more elementary terms, this says that elements of 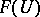 can be uniquely "patched together" from compatible families of elements of
can be uniquely "patched together" from compatible families of elements of 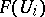 .)
.)
Abstracting from this definition, one defines a pre-sheaf on an arbitrary category 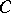 to be a functor
to be a functor 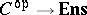 . In order to define the notion of a sheaf on
. In order to define the notion of a sheaf on 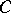 , one needs a structure
, one needs a structure  , called a Grothendieck topology, assigning to each object
, called a Grothendieck topology, assigning to each object 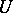 of
of 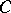 a set
a set 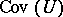 of coverings of
of coverings of 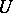 , which are families of morphisms
, which are families of morphisms 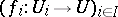 with common codomain
with common codomain 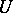 . The assignment
. The assignment 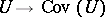 is required to satisfy certain conditions, of which the most important is the "pullback-stability" condition:
is required to satisfy certain conditions, of which the most important is the "pullback-stability" condition:
a) If 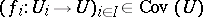 and
and 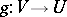 is any morphism, there exists
is any morphism, there exists 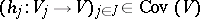 such that, for each
such that, for each 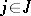 , the composite
, the composite 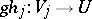 factors through some
factors through some 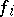 .
.
Other closure conditions which are commonly imposed, though they are less important for the purpose of defining the category of sheaves, are:
b) for every object 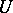 of
of 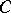 , the singleton family
, the singleton family 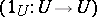 is in
is in 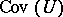 ;
;
c) if 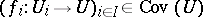 and, for each
and, for each 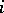 ,
, 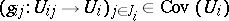 , then the family of all composites
, then the family of all composites 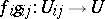 (
(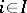 ,
, 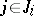 ) is in
) is in 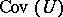 ;
;
d) any family containing a family in 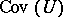 is in
is in 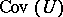 .
.
In defining the notion of a Grothendieck topology, many authors require the underlying category 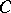 to have pullbacks; in this case condition a) can be formulated more simply, but the restriction is not essential.
to have pullbacks; in this case condition a) can be formulated more simply, but the restriction is not essential.
Given a Grothendieck topology  on
on 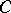 , a pre-sheaf
, a pre-sheaf  on
on 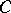 is called a
is called a  -sheaf (or simply a sheaf) if, for every family
-sheaf (or simply a sheaf) if, for every family 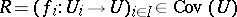 , the canonical mapping
, the canonical mapping 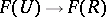 induced by the
induced by the 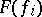 is bijective, where
is bijective, where 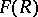 denotes the set of families
denotes the set of families 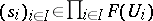 which are compatible in the sense that, whenever mappings
which are compatible in the sense that, whenever mappings 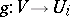 and
and 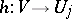 satisfy
satisfy 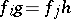 , then
, then 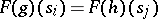 . (Again, this definition can be stated more simply if the pullbacks
. (Again, this definition can be stated more simply if the pullbacks 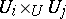 all exist in
all exist in 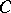 , but this is inessential.) Sheaves of Abelian groups, rings and other structures can be defined similarly.
, but this is inessential.) Sheaves of Abelian groups, rings and other structures can be defined similarly.
The full subcategory of the functor category 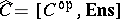 whose objects are sheaves (for a given topology
whose objects are sheaves (for a given topology  ) is denoted by
) is denoted by 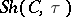 or
or 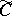 . Provided the site
. Provided the site 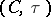 satisfies an appropriate smallness condition,
satisfies an appropriate smallness condition, 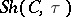 is a topos, and is a reflective subcategory of
is a topos, and is a reflective subcategory of 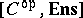 , the reflector preserving finite limits. Conversely, any reflective subcategory of
, the reflector preserving finite limits. Conversely, any reflective subcategory of 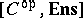 whose reflector preserves finite limits may be represented as
whose reflector preserves finite limits may be represented as 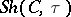 for a suitable Grothendieck topology
for a suitable Grothendieck topology  on
on  (Giraud's little theorem). Categories equivalent to one of the form
(Giraud's little theorem). Categories equivalent to one of the form 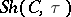 are commonly called Grothendieck toposes (see Topos); they can be characterized (Giraud's big theorem) as categories
are commonly called Grothendieck toposes (see Topos); they can be characterized (Giraud's big theorem) as categories 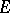 with the following properties:
with the following properties:
1) 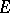 has finite limits;
has finite limits;
2) 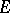 has arbitrary small coproducts, which are disjoint and universal (i.e. stable under pullback);
has arbitrary small coproducts, which are disjoint and universal (i.e. stable under pullback);
3) equivalence relations in 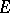 are effective, and have universal co-equalizers;
are effective, and have universal co-equalizers;
4) 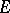 has small
has small 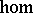 -sets and a small set of generators.
-sets and a small set of generators.
Alternatively, a Grothendieck topos may be characterized as a category 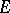 with a set of generators, which is equivalent to the category of sheaves on itself when it is equipped with the canonical topology (the largest topology for which all representable functors are sheaves, cf. Representable functor).
with a set of generators, which is equivalent to the category of sheaves on itself when it is equipped with the canonical topology (the largest topology for which all representable functors are sheaves, cf. Representable functor).
The category of Abelian groups in a Grothendieck topos (equivalently, the category of sheaves of Abelian groups on a site) is a Grothendieck category, which makes it possible to define sheaf cohomology on a site; the cohomology groups 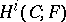 , where
, where 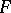 is a sheaf of Abelian groups on
is a sheaf of Abelian groups on 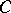 , are (the values at
, are (the values at 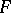 of) the derived functors of the global section functor
of) the derived functors of the global section functor 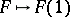 (where
(where 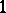 is a terminal object of
is a terminal object of 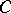 ).
).
Sites were first introduced in algebraic geometry [a1], [a2], in connection with the étale topology of a scheme and similar topologies used to define cohomology theories studied by algebraic geometers.
Subsequently, they have been found useful in other contexts, notably in the construction of models for synthetic differential geometry [a3], [a4].
References
| [a1] | J. Giraud, "Analysis situs" , Sem. Bourbaki (1963) pp. Exp. 256 |
| [a2] | M. Artin, A. Grothendieck, J.-L. Verdier, "Théorie des topos et cohomologie étale des schémas" , SGA 4 , Lect. notes in math. , 269; 270; 305 , Springer (1972) |
| [a3] | A. Kock, "Synthetic differential geometry" , Cambridge Univ. Press (1981) |
| [a4] | I. Moerdijk, G.E. Reyes, "Models for smooth infinitesimal analysis" , Springer (1990) |
| [a5] | P.T. Johnstone, "Topos theory" , Acad. Press (1977) |
Site. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Site&oldid=12852