Bahadur efficiency
The large sample study of test statistics in a given hypotheses testing problem is commonly based on the following concept of asymptotic Bahadur efficiency [a1], [a2] (cf. also Statistical hypotheses, verification of). Let  and
and  be the parametric sets corresponding to the null hypothesis and its alternative, respectively. Assume that large values of a test statistic (cf. Test statistics)
be the parametric sets corresponding to the null hypothesis and its alternative, respectively. Assume that large values of a test statistic (cf. Test statistics)  based on a random sample
based on a random sample  give evidence against the null hypothesis. For a fixed
give evidence against the null hypothesis. For a fixed  and a real number
and a real number  , put
, put  and let
and let  . The random quantity
. The random quantity  is the
is the  -value corresponding to the statistic
-value corresponding to the statistic 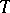 when
when  is the true parametric value. For example, if
is the true parametric value. For example, if  , the null hypothesis
, the null hypothesis  is rejected at the significance level
is rejected at the significance level 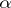 . If for
. If for  with
with  -probability one,
-probability one,
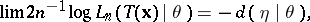 |
then  is called the Bahadur exact slope of
is called the Bahadur exact slope of  . The larger the Bahadur exact slope, the faster the rate of decay of the
. The larger the Bahadur exact slope, the faster the rate of decay of the 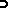 -value under the alternative. It is known that for any
-value under the alternative. It is known that for any  ,
,  , where
, where  is the information number corresponding to
is the information number corresponding to 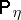 and
and  . A test statistic
. A test statistic  is called Bahadur efficient at
is called Bahadur efficient at 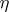 if
if
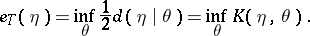 |
The concept of Bahadur efficiency allows one to compare two (sequences of) test statistics  and
and 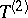 from the following perspective. Let
from the following perspective. Let  ,
,  , be the smallest sample size required to reject
, be the smallest sample size required to reject  at the significance level
at the significance level 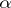 on the basis of a random sample
on the basis of a random sample  when
when 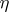 is the true parametric value. The ratio
is the true parametric value. The ratio  gives a measure of relative efficiency of
gives a measure of relative efficiency of  to
to  . To reduce the number of arguments
. To reduce the number of arguments 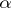 ,
,  and
and  , one usually considers the random variable which is the limit of this ratio, as
, one usually considers the random variable which is the limit of this ratio, as  . In many situations this limit does not depend on
. In many situations this limit does not depend on  , so it represents the efficiency of
, so it represents the efficiency of  against
against  at
at  with the convenient formula
with the convenient formula
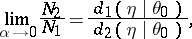 |
where 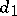 and
and 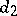 are the corresponding Bahadur slopes.
are the corresponding Bahadur slopes.
To evaluate the exact slope, the following result ([a2], Thm. 7.2) is commonly used. Assume that for any  with
with 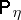 -probability one as
-probability one as  ,
,  and the limit
and the limit  exists for
exists for 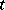 taking values in an open interval and is a continuous function there. Then the exact slope of
taking values in an open interval and is a continuous function there. Then the exact slope of  at
at  has the form
has the form  . See [a4] for generalizations of this formula.
. See [a4] for generalizations of this formula.
The exact Bahadur slopes of many classical tests have been found. See [a3].
References
| [a1] | R.R. Bahadur, "Rates of convergence of estimates and tests statistics" Ann. Math. Stat. , 38 (1967) pp. 303–324 |
| [a2] | R.R. Bahadur, "Some limit theorems in statistics" , Regional Conf. Ser. Applied Math. , SIAM (1971) |
| [a3] | Ya.Yu. Nikitin, "Asymptotic efficiency of nonparametric tests" , Cambridge Univ. Press (1995) |
| [a4] | L.J. Gleser, "Large deviation indices and Bahadur exact slopes" Statistics and Decision , 1 (1984) pp. 193–204 |
Bahadur efficiency. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bahadur_efficiency&oldid=12851