Segal-Shale-Weil representation

A representation of groups arising in both number theory and in physics. For number theorists, the seminal paper is that of A. Weil, [a1]. He cites earlier papers of I. Segal and D. Shale as precedents, and the deep work of C.L. Siegel on theta-series as inspiration.

Let be a group with centre such that is Abelian, and let be a unitary character of (cf. also Character of a group). If , choose representatives and note that is independent of the choice of representatives. This is a skew-symmetric bilinear pairing . One assumes that this pairing is non-degenerate. The Stone–von Neumann theorem asserts that 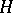has a unique irreducible representation with central character 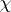. Furthermore, the representation may be constructed as follows. Let 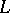be a Lagrangian subgroup, that is, any subgroup of containing 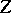such that 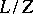is a maximal subgroup of 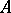on which the form 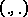is trivial. Extend to 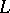in an arbitrary manner, then induce. This gives a model for .

Let be a group of automorphisms of 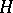which acts trivially on (cf. also Automorphism). If , the Stone–von Neumann theorem implies that . Let 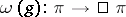be an intertwining mapping, well defined up to constant multiple (cf. also Intertwining operator). Then is a projective representation of .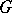

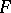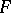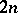For example, let be a local field and let be a vector space over endowed with a non-degenerate skew-symmetric bilinear form . Its dimension is even, and the automorphism group of the form is the symplectic group . One can construct a "Heisenberg group" with the multiplication 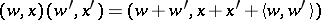. Choosing any non-trivial additive character of , let . Then the hypotheses of the Stone–von Neumann theorem are satisfied. As the Lagrangian subgroup of one may take , where 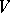is any maximal isotropic subspace of 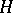. Then the induced model of 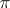described above may be realized as the Schwartz space . The Segal–Shale–Weil representation is the resulting projective representation of 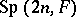. It may be interpreted as a genuine representation of a covering group 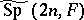, the so-called metaplectic group.

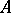Now let be a global field, its adèle ring (cf. also Adèle), and let 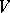and 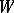be as before. Then one may construct a similar representation 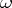of 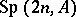on the Schwartz space 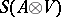. If , let . This linear form is invariant under the action of , generalizing the Poisson summation formula. This implies that the representation is automorphic. The corresponding automorphic forms are theta-functions (cf. Theta-function), having their historical origins in the work of C.G.J. Jacobi and Siegel. As Weil observed, the automorphicity of this representation is closely related to the quadratic reciprocity law.

Later authors, notably R. Howe [a2], have emphasized the theory of dual reductive pairs. When a pair of reductive groups embeds in 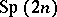, each being the centralizer of the other (cf. also Centralizer), then 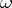sets up a correspondence between representations of and representations of 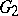. This works at the level of automorphic forms and gives instances of Langlands functoriality, including some historically important ones such as quadratic base change (cf. also Base change). See [a3]. The use of the Weil representation in [a4] to construct automorphic forms and representations may be understood as arising from the dual reductive pairs 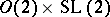and 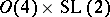. The dual pair underlies the important work of J.-L. Waldspurger [a5] on automorphic forms of half-integral weight.

In recent years (as of 2000) it has been noted that since the Segal–Shale–Weil representation is the minimal representation of 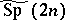, that is, the representation with smallest Gel'fand–Kirillov dimension, minimal representations of other groups can play a similar role. Many interesting examples may be found in the exceptional groups (cf. also Lie algebra, exceptional). The possibly first paper where this phenomenon was noted was [a6]. Many interesting examples come from the exceptional groups. There is much current literature on this subject, but for typical papers see [a7] and [a8]. Dual pairs in the exceptional groups were classified in [a9].

For further references see [a10].

References

[a1]	A. Weil, "Sur certains groupes d'opérateurs unitaires" Acta Math. , 111 (1964) pp. 143–211 (Also: Collected Works, Vol. 3)
[a2]	R.E. Howe, "-series and invariant theory" , Automorphic forms, representations and -functions , Proc. Symp. Pure Math. , 33:1 , Amer. Math. Soc. (1977)
[a3]	S. Rallis, "Langlands' functoriality and the Weil representation" Amer. J. Math. , 104 : 3 (1982) pp. 469–515
[a4]	H. Jacquet, R.P. Langlands, "Automorphic forms on 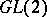" , Lecture Notes in Mathematics , 114 , Springer (1970)
[a5]	J.-L. Waldspurger, "Sur les coefficients de Fourier des formes modulaires de poids demi-entier" J. Math. Pures Appl. , 60 (1981) pp. 375–484
[a6]	D. Kazhdan, "The minimal representation of 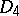" , Operator Algebras, Unitary Representations, Enveloping Algebras, and Invariant Theory (Paris, 1989) , Birkhäuser (1990) pp. 125–158
[a7]	D. Ginzburg, S. Rallis, D. Soudry, "A tower of theta correspondences for 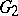" Duke Math. J. , 88 (1997) pp. 537–624
[a8]	B.H. Gross, G. Savin, "The dual pair 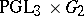" Canad. Math. Bull. , 40 : 3 (1997) pp. 376–384
[a9]	H. Rubenthaler, "Les paires duales dans les algèbres de Lie réductives" Astérisque , 219 (1994)
[a10]	D. Prasad, "A brief survey on the theta correspondence" , Number theory , Contemp. Math. , 210 , Amer. Math. Soc. (1998) pp. 171–193