Structure space

of a ring

The set of all its primitive ideals with the following topology: A subset is closed if 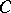contains every ideal that contains the intersection of all ideals from 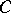(see Zariski topology). The structure space of a ring 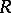is homeomorphic to the structure space of the quotient ring 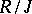, where 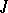is the Jacobson radical. A structure space is a 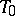-space; if all primitive ideals of the ring are maximal, then the structure space is a 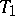-space. The structure space of a ring with a unit is compact. The structure space of a biregular ring (see Regular ring (in the sense of von Neumann)) is locally compact and totally disconnected. It is used to represent a biregular ring in the form of a ring of continuous functions with compact supports.

References

[1]	N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956)

Comments

This is an extension of the notion of the spectrum space of maximal ideals of a commutative ring (cf. Spectrum of a ring).

References

[a1]	K.R. Goodearl, "Von Neumann regular rings" , Pitman (1979)