Replica of an endomorphism

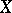of a finite-dimensional vector space 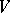over a field 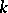of characteristic 0

An element of the smallest algebraic Lie subalgebra 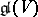containing 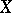(see Lie algebra, algebraic). An endomorphism 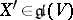is a replica of the endomorphism 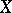if and only if each tensor over 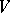that is annihilated by 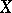is also annihilated by .

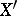Each replica of an endomorphism 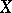can be written as a polynomial in 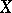with coefficients from the field 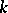and without absolute term. The semi-simple and nilpotent components of an endomorphism 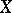(see Jordan decomposition, 2) are replicas of it. A subalgebra of the Lie algebra 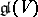is algebraic if and only if it contains all replicas of all its elements. An endomorphism 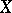of a space 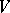is nilpotent if and only if 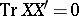for any replica 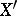of .

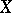Let 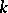be an algebraically closed field, let 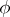be an automorphism of 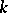, let 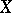be a semi-simple endomorphism of the space 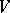, and let be an endomorphism of 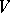such that any eigenvector of 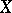corresponding to an eigenvalue 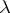is also an eigenvector for 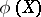, but corresponding to the eigenvalue 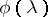. An endomorphism 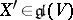is a replica of the endomorphism 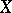if and only if 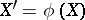for some automorphism 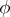of the field .

References

[1]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French)
[2]	, Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Secr. Math. Univ. Paris (1955)
[3]	C. Chevalley, "Théorie des groupes de Lie" , 2 , Hermann (1951)

References

[a1]	N. Bourbaki, "Groupes et algèbres de Lie" , Hermann (1975) pp. Chapts. VII-VIII