Subgroup
A non-empty subset 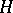 of a group
of a group 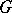 which itself is a group with respect to the operation defined on
which itself is a group with respect to the operation defined on 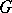 . A subset
. A subset 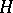 of a group
of a group 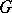 is a subgroup of
is a subgroup of 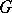 if and only if: 1)
if and only if: 1) 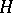 contains the product of any two elements from
contains the product of any two elements from 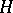 ; and 2)
; and 2) 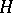 contains together with any element
contains together with any element 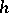 the inverse
the inverse 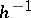 . In the cases of finite and periodic groups, condition 2) is superfluous.
. In the cases of finite and periodic groups, condition 2) is superfluous.
The subset of a group G consisting of the element 1 only is clearly a subgroup; it is called the unit subgroup of 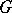 and is usually denoted by
and is usually denoted by  . Also,
. Also, 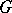 itself is a subgroup. A subgroup different from
itself is a subgroup. A subgroup different from 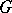 is called a proper subgroup of
is called a proper subgroup of 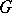 . A proper subgroup of an infinite group can be isomorphic to the group itself. The group
. A proper subgroup of an infinite group can be isomorphic to the group itself. The group 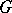 itself and the subgroup
itself and the subgroup 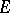 are called improper subgroups of
are called improper subgroups of 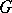 , while all the others are called proper ones.
, while all the others are called proper ones.
The set-theoretic intersection of any two (or any set of) subgroups of a group 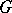 is a subgroup of
is a subgroup of 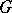 . The intersection of all subgroups of
. The intersection of all subgroups of 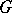 containing all elements of a certain non-empty set
containing all elements of a certain non-empty set 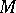 is called the subgroup generated by the set
is called the subgroup generated by the set 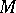 and is denoted by
and is denoted by 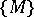 . If
. If 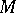 consists of one element
consists of one element  , then
, then 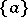 is called the cyclic subgroup of the element
is called the cyclic subgroup of the element  . A group that coincides with one of its cyclic subgroups is called a cyclic group.
. A group that coincides with one of its cyclic subgroups is called a cyclic group.
A set-theoretic union of subgroups is, in general, not a subgroup. By the join of subgroups 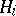 ,
, 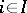 , one means the subgroup generated by the union of the sets
, one means the subgroup generated by the union of the sets 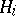 .
.
The product of two subsets 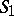 and
and 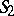 of a group
of a group 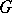 is the set consisting of all possible (different) products
is the set consisting of all possible (different) products 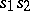 , where
, where 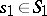 ,
, 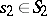 . The product of two subgroups
. The product of two subgroups 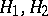 is a subgroup if and only if
is a subgroup if and only if 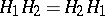 , and in that case the product
, and in that case the product 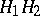 coincides with the subgroup generated by
coincides with the subgroup generated by 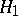 and
and 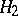 (i.e. with the join of
(i.e. with the join of 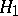 and
and 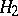 ).
).
A homomorphic image of a subgroup is a subgroup. If a group 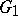 is isomorphic to a subgroup
is isomorphic to a subgroup 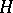 of a group
of a group 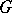 , one says that
, one says that 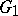 can be imbedded in
can be imbedded in 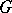 (as groups). If one is given two groups and each of them is isomorphic to a proper subgroup of the other, it does not necessarily follow that these groups themselves are isomorphic (cf. also Homomorphism; Isomorphism).
(as groups). If one is given two groups and each of them is isomorphic to a proper subgroup of the other, it does not necessarily follow that these groups themselves are isomorphic (cf. also Homomorphism; Isomorphism).
Comments
References
| [a1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [a2] | M. Hall jr., "The theory of groups" , Macmillan (1959) pp. 124 |
Subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subgroup&oldid=12801