Algebraic system
A set with operations and relations defined on it. An algebraic system is one of the basic mathematical concepts and its general theory has been developed in depth. This was done in the 1950s, and the work took place on the interface between algebra and mathematical logic.
Fundamental concepts.
An algebraic system is an object 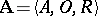 consisting of a non-empty set
consisting of a non-empty set 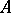 , a family
, a family 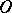 of algebraic operations (cf. Algebraic operation)
of algebraic operations (cf. Algebraic operation) 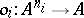 (
(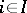 ) and a family
) and a family 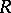 of relations (cf. Relation)
of relations (cf. Relation) 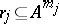 (
(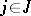 ) defined on
) defined on 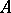 . The indices
. The indices 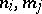 of the Cartesian powers of
of the Cartesian powers of 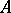 under consideration are assumed to be non-negative integers and are said to be the arities of the respective operations and relations. The set
under consideration are assumed to be non-negative integers and are said to be the arities of the respective operations and relations. The set 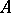 is called the carrier or the underlying set of the algebraic system
is called the carrier or the underlying set of the algebraic system 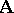 , while its elements are called the elements of this system. The cardinality
, while its elements are called the elements of this system. The cardinality 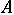 of
of 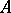 is said to be the cardinality or order of the algebraic system
is said to be the cardinality or order of the algebraic system 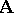 . The image
. The image 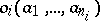 of the element
of the element 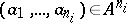 under the mapping
under the mapping 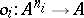 is called the value of the operation
is called the value of the operation 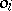 at the point
at the point 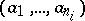 . Similarly, if
. Similarly, if 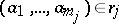 , then one says that the elements
, then one says that the elements 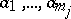 of
of  are in relation
are in relation 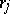 , and one writes
, and one writes 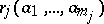 . The operations
. The operations 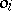 (
(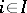 ) and the relations
) and the relations  (
(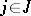 ), unlike other operations and relations that may be defined on
), unlike other operations and relations that may be defined on  , are called basic or primitive.
, are called basic or primitive.
The pair of families 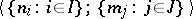 is called the type of the algebraic system
is called the type of the algebraic system  . Two algebraic systems
. Two algebraic systems 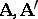 have the same type if
have the same type if 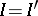 ,
, 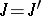 and
and 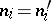 ,
, 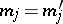 for all
for all 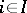 ,
, 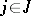 . Basic operations
. Basic operations 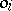 ,
, 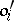 and basic relations
and basic relations 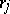 ,
,  of two algebraic systems
of two algebraic systems 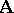 ,
,  of the same type, with identical indices in
of the same type, with identical indices in 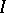 ,
, 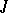 respectively, are called similar.
respectively, are called similar.
An algebraic system 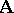 is called finite if the set
is called finite if the set 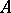 is finite and it is called of finite type if the set
is finite and it is called of finite type if the set 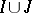 is finite. An algebraic system
is finite. An algebraic system 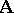 of finite type is written as
of finite type is written as 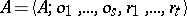 .
.
An algebraic system 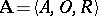 is called a universal algebra or an algebra if the set
is called a universal algebra or an algebra if the set 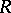 of its basic relations is empty, and it is called a model (in logic) or a relational system if the set
of its basic relations is empty, and it is called a model (in logic) or a relational system if the set 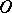 of basic operations is empty. Classical algebraic systems are groups, rings, linear spaces, linear algebras, totally ordered sets, totally ordered groups, lattices, etc.
of basic operations is empty. Classical algebraic systems are groups, rings, linear spaces, linear algebras, totally ordered sets, totally ordered groups, lattices, etc.
A non-empty subset 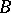 of the underlying set
of the underlying set  of an algebraic system
of an algebraic system 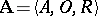 is called closed if for any elements
is called closed if for any elements 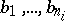 of
of 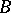 the value
the value 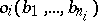 of each basic operation
of each basic operation 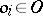 also belongs to
also belongs to 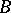 . By considering the operations of
. By considering the operations of 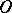 and the relations of
and the relations of 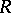 on a closed subset
on a closed subset 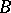 , one obtains an algebraic system
, one obtains an algebraic system 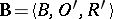 which is of the same type as the given algebraic system and is called a subsystem of the algebraic system
which is of the same type as the given algebraic system and is called a subsystem of the algebraic system 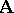 . Subsystems of algebras are called subalgebras, while subsystems of models are called submodels. The concept of a subalgebra strongly depends on the set of basic operations of the algebra under consideration. Thus, a groupoid
. Subsystems of algebras are called subalgebras, while subsystems of models are called submodels. The concept of a subalgebra strongly depends on the set of basic operations of the algebra under consideration. Thus, a groupoid  is an algebra of type
is an algebra of type 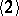 , i.e. an algebra with one basic operation
, i.e. an algebra with one basic operation 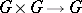 . A groupoid
. A groupoid  with a distinguished unit
with a distinguished unit  is an algebra of type
is an algebra of type 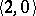 , the distinguished element of which has the property
, the distinguished element of which has the property 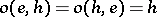 for all
for all 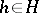 with respect to the basic operation
with respect to the basic operation  . For this reason any subgroupoid of a groupoid
. For this reason any subgroupoid of a groupoid  with a distinguished unit
with a distinguished unit  contains
contains  , while a subgroupoid of a groupoid
, while a subgroupoid of a groupoid 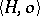 does not necessarily contain
does not necessarily contain  . Unlike algebras, any non-empty subset of a model may be considered as a submodel.
. Unlike algebras, any non-empty subset of a model may be considered as a submodel.
An algebraic system 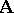 is isomorphic to an algebraic system
is isomorphic to an algebraic system 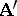 of the same type if there exists a one-to-one mapping
of the same type if there exists a one-to-one mapping 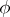 of the set
of the set 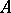 into the set
into the set  such that
such that
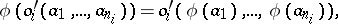 | (1) |
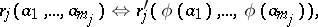 | (2) |
holds for all 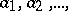 of
of 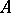 and for all
and for all 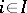 ,
, 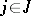 . A mapping
. A mapping 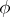 possessing these properties is called an isomorphism.
possessing these properties is called an isomorphism.
In the following, a class of algebraic systems will be understood to mean only an abstract class, i.e. a class of algebraic systems of the same type which, whenever it contains a system 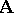 , also contains all systems isomorphic to
, also contains all systems isomorphic to 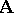 . In considering a class
. In considering a class 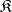 of algebraic systems, all systems in this class are usually written in a definite signature, as follows. Let the type of the class
of algebraic systems, all systems in this class are usually written in a definite signature, as follows. Let the type of the class 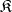 be
be 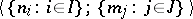 . To each
. To each 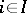 is assigned some symbol
is assigned some symbol 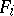 , called a functional, while to each
, called a functional, while to each 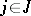 is assigned a symbol
is assigned a symbol 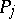 , called a predicate. If an algebraic system
, called a predicate. If an algebraic system 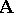 belongs to the class
belongs to the class 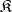 and if
and if 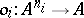 is a basic operation in it, then the element
is a basic operation in it, then the element 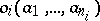 of
of 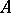 is written as
is written as  . Similarly, if
. Similarly, if 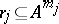 is a basic relation in
is a basic relation in 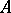 and the element
and the element 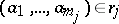 , then one writes
, then one writes 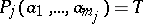 (true) or simply
(true) or simply 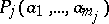 . If, on the other hand,
. If, on the other hand, 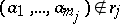 , one writes
, one writes 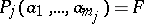 (false) or
(false) or 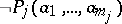 . Let
. Let 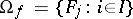 ,
, 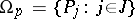 and let
and let  be the mapping of the union
be the mapping of the union 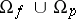 into the set of natural numbers
into the set of natural numbers 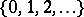 , defined by the formulas
, defined by the formulas 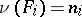 (
(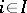 ),
), 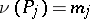 (
(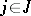 ). The object
). The object 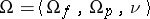 is the signature of the class
is the signature of the class 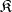 . A finite signature is written as a string
. A finite signature is written as a string 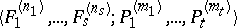 or, more briefly,
or, more briefly, 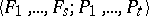 . An algebraic system
. An algebraic system 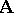 , written in the signature
, written in the signature  , is known as an
, is known as an  -system and is denoted by
-system and is denoted by 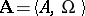 .
.
The conditions (1) and (2) for an isomorphism of the systems 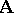 and
and 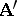 become simplified if the systems are considered in one signature
become simplified if the systems are considered in one signature  . Thus, if
. Thus, if 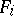 (
(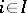 ) and
) and 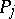 (
(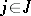 ) are the signature symbols, equations (1) and (2) assume the form
) are the signature symbols, equations (1) and (2) assume the form
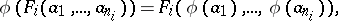 | (3) |
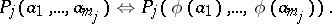 | (4) |
A homomorphism of an  -system
-system 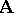 into an
into an  -system
-system 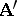 is any mapping
is any mapping 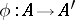 which fulfills both condition (3) and the condition
which fulfills both condition (3) and the condition
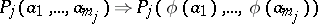 | (5) |
for all  and for all
and for all 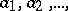 of
of 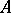 . A homomorphism
. A homomorphism  is called strong if, for any elements
is called strong if, for any elements 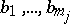 of
of  and for any predicate symbol
and for any predicate symbol 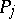 of
of 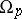 , the relation
, the relation 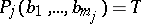 implies the existence in
implies the existence in 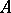 of pre-images
of pre-images 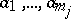 of the elements
of the elements 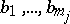 such that
such that 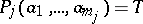 . The concepts of a homomorphism and of a strong homomorphism of algebras are identical. Models have homomorphisms that are not strong, and have one-to-one homomorphisms that are not isomorphisms. Under a homomorphism
. The concepts of a homomorphism and of a strong homomorphism of algebras are identical. Models have homomorphisms that are not strong, and have one-to-one homomorphisms that are not isomorphisms. Under a homomorphism 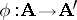 , images of subsystems of
, images of subsystems of 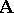 are subsystems in
are subsystems in  ; and non-empty complete pre-images of subsystems of
; and non-empty complete pre-images of subsystems of 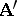 are subsystems in
are subsystems in 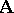 .
.
An equivalence relation 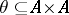 is called a congruence of the
is called a congruence of the  -system
-system 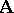 if
if
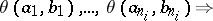 |
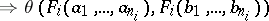 |
for all 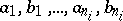 of
of  and all
and all 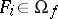 . For each homomorphism
. For each homomorphism 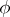 of an algebraic system
of an algebraic system 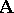 the binary relation
the binary relation 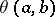 which holds if and only if
which holds if and only if 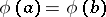 is a congruence in
is a congruence in  , called its kernel congruence. For any congruence
, called its kernel congruence. For any congruence 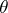 of an
of an  -system
-system 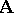 and for each element
and for each element  the set
the set  is called a coset of the algebraic system
is called a coset of the algebraic system 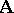 by the congruence
by the congruence 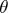 . On the assumption that, for each
. On the assumption that, for each 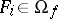 ,
, 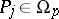 ,
,
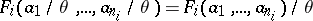 |
and
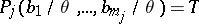 |
if and only if there exist elements 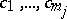 in
in 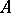 such that
such that 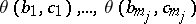 and
and 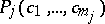 , one obtains the algebraic system
, one obtains the algebraic system 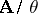 , which is of the same type as the given system; it is called the quotient system of the algebraic system
, which is of the same type as the given system; it is called the quotient system of the algebraic system 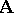 by the congruence
by the congruence 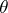 . For each congruence
. For each congruence 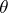 of an algebraic system
of an algebraic system 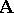 the canonical mapping
the canonical mapping 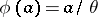 (
(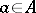 ) is a homomorphism of
) is a homomorphism of 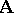 onto the quotient system
onto the quotient system 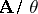 for which the given congruence
for which the given congruence 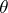 is the kernel congruence. If
is the kernel congruence. If 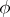 is a homomorphism of an algebraic system
is a homomorphism of an algebraic system  into an algebraic system
into an algebraic system 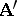 and
and 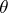 is the kernel congruence for
is the kernel congruence for 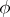 , then the mapping
, then the mapping 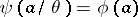 is a homomorphism of the quotient system
is a homomorphism of the quotient system 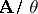 into the algebraic system
into the algebraic system 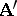 . If the homomorphism
. If the homomorphism 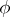 is strong,
is strong, 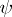 is an isomorphism.
is an isomorphism.
The Cartesian product of  -systems
-systems  ,
, 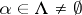 , is the
, is the  -system
-system 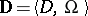 in which
in which 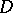 is the Cartesian product of the underlying sets
is the Cartesian product of the underlying sets 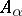 (
(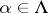 ) and the basic operations and the basic relations on
) and the basic operations and the basic relations on 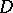 are given by the conditions:
are given by the conditions:  (
(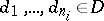 ,
, 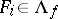 ) is the element
) is the element 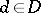 with coordinates
with coordinates 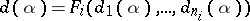 (
(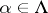 ),
), 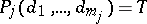 (
(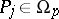 ) if and only if
) if and only if 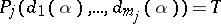 for all
for all 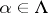 .
.
A language of the first order.
The basic formal language of the theory of algebraic systems is the first-order language 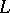 which is constructed as follows. The alphabet of the language
which is constructed as follows. The alphabet of the language 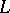 in the given signature
in the given signature 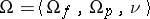 ,
, 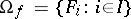 ,
, 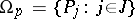 , consists of the object variables
, consists of the object variables 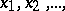 the function symbols
the function symbols 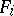 (
(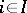 ), the predicate symbols
), the predicate symbols 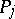 (
( ), the logical connectives
), the logical connectives
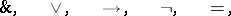 |
the quantifiers:
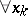 — "for each element xk" ;
— "for each element xk" ;
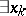 — "there exists an element xk" ;
— "there exists an element xk" ;
and the auxiliary symbols: brackets and commas. The (first-order) properties of  -systems are expressed by finite sequences of alphabet symbols, or words, constructed in accordance with specific rules and known as terms and formulas. It is inductively assumed that each word of the form
-systems are expressed by finite sequences of alphabet symbols, or words, constructed in accordance with specific rules and known as terms and formulas. It is inductively assumed that each word of the form 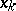 or
or 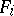 is a term if
is a term if 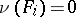 ; if
; if 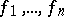 are terms and if
are terms and if 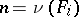 , then
, then 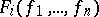 is also a term.
is also a term.
If  is an
is an  -system and if
-system and if 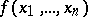 is a term of the signature
is a term of the signature  containing object variables
containing object variables  , then if one replaces
, then if one replaces  by some elements
by some elements  in
in 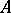 , and executes the operations in
, and executes the operations in 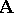 on the latter elements corresponding to the symbols of
on the latter elements corresponding to the symbols of  forming part of this term, then one obtains an element
forming part of this term, then one obtains an element 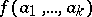 from
from  , which is called the value of the term
, which is called the value of the term 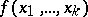 for
for  . If
. If  is a homomorphism of an
is a homomorphism of an  -system
-system 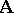 into an
into an  -system
-system  , then
, then
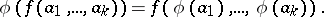 |
The concept of a formula of the signature  , and of free and bound object variables in it, is also defined inductively:
, and of free and bound object variables in it, is also defined inductively:
1) If 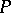 is any predicate symbol for
is any predicate symbol for  or the equality sign
or the equality sign  ,
, 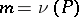 or 2 respectively, and if
or 2 respectively, and if 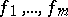 are arbitrary terms of the signature
are arbitrary terms of the signature  , then the word
, then the word 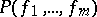 is a formula in which all object variables are free.
is a formula in which all object variables are free.
2) If 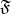 is a formula, so is
is a formula, so is 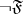 . Free (bound) object variables in the formula
. Free (bound) object variables in the formula 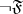 are those and only those variables which are free (bound) in
are those and only those variables which are free (bound) in 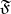 .
.
3) If 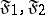 are formulas and if the object variables which form part of both formulas are free in both formulas, then the words
are formulas and if the object variables which form part of both formulas are free in both formulas, then the words
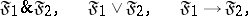 | (6) |
are also formulas.
Object variables which are free (bound) in at least one of the formulas 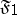 ,
, 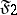 are called free (bound) in the formulas (6) as well.
are called free (bound) in the formulas (6) as well.
4) If an object variable 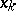 occurs free in a formula
occurs free in a formula 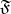 , then the words
, then the words 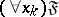 ,
, 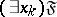 are again formulas in which the variable
are again formulas in which the variable 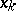 is bound, while all the other object variables which occur free or bound in the formula
is bound, while all the other object variables which occur free or bound in the formula  remain free or bound in the formulas
remain free or bound in the formulas 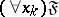 ,
, 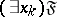 as well.
as well.
Let an  -system
-system 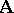 and a formula
and a formula 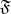 of the signature
of the signature  be given. If one now assigns to all free object variables
be given. If one now assigns to all free object variables  from
from 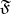 some values
some values  from
from 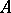 and if one interprets the function and the predicate symbols forming part of
and if one interprets the function and the predicate symbols forming part of 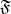 as the respective basic operations and basic relations in
as the respective basic operations and basic relations in 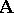 , then one obtains a definite statement which may be true or false. One accordingly assigns to the formula
, then one obtains a definite statement which may be true or false. One accordingly assigns to the formula 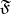 the value
the value 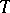 or
or 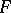 , for
, for  denoted by
denoted by 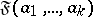 . If
. If 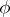 is an isomorphic mapping of an
is an isomorphic mapping of an  -system
-system 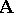 into an
into an  -system
-system 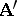 , then
, then
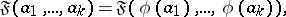 |
for all  from
from  .
.
A formula 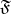 is called closed if it contains no free object variables. For any closed formula
is called closed if it contains no free object variables. For any closed formula 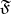 of the signature
of the signature  and any
and any  -system
-system 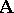 one may speak of
one may speak of 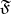 being true or false in
being true or false in 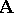 . A set
. A set 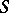 of closed formulas of a given signature
of closed formulas of a given signature  is said to be realizable or consistent if there exists an
is said to be realizable or consistent if there exists an  -system in which all formulas from
-system in which all formulas from 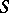 are true.
are true.
The compactness theorem or the Gödel–Mal'tsev theorem states: If each finite subset of an infinite set 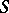 of closed formulas of a given signature
of closed formulas of a given signature  is realizable, then the entire set
is realizable, then the entire set 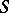 is realizable as well.
is realizable as well.
Axiomatizable classes.
Let 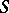 be some set of closed formulas of a signature
be some set of closed formulas of a signature  . The class of all
. The class of all  -systems in which all formulas of
-systems in which all formulas of 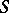 are true will be denoted by
are true will be denoted by 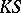 . The set
. The set 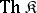 of all closed formulas of a signature
of all closed formulas of a signature  which are true in all
which are true in all  -systems of the given class
-systems of the given class 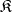 , is called the elementary theory of
, is called the elementary theory of 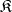 . In particular, if
. In particular, if 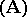 is the class of
is the class of  -systems isomorphic to the given
-systems isomorphic to the given  -system
-system 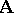 , then
, then 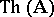 is said to be the elementary theory of the
is said to be the elementary theory of the  -system
-system 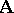 and is simply denoted by
and is simply denoted by 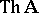 . A class
. A class 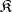 of
of  -systems is said to be axiomatizable if
-systems is said to be axiomatizable if 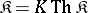 . A class
. A class 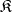 of
of  -systems is axiomatizable if and only if there exists a set
-systems is axiomatizable if and only if there exists a set 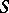 of closed formulas of the signature
of closed formulas of the signature  such that
such that  .
.
Along with the general concept of axiomatizability, axiomatizability using first-order formulas of a special kind may also be considered. The special formulas of a given signature which are the most important in algebra are:
Identities — the formulas
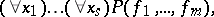 |
where 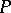 is some predicate symbol from
is some predicate symbol from  or the equality sign
or the equality sign  , and
, and 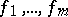 are terms of the signature
are terms of the signature  in
in  .
.
Quasi-identities — the formulas
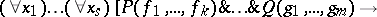 |
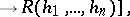 |
where 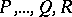 are certain predicate symbols from
are certain predicate symbols from 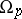 or equality signs, while
or equality signs, while 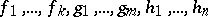 are terms of the signature
are terms of the signature  in
in  .
.
Universal formulas — the formulas 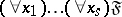 , where
, where 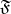 is a formula of the signature
is a formula of the signature  not containing quantifiers.
not containing quantifiers.
If a set 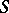 of identities (quasi-identities or universal formulas) of a signature
of identities (quasi-identities or universal formulas) of a signature  is given, then the class
is given, then the class  is known as a variety (quasi-variety or universal class) of
is known as a variety (quasi-variety or universal class) of  -systems.
-systems.
Birkhoff's theorem: A non-empty class 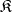 of
of  -systems is a variety if and only if it is closed with respect to subsystems, Cartesian products and homomorphic images.
-systems is a variety if and only if it is closed with respect to subsystems, Cartesian products and homomorphic images.
If 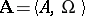 is some
is some  -system, then, by exchanging each function symbol
-system, then, by exchanging each function symbol 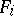 from
from 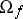 for a predicate symbol
for a predicate symbol 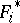 of arity
of arity 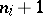 (higher by one) and putting, for elements
(higher by one) and putting, for elements 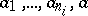 from
from 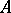
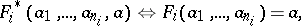 |
one obtains a model 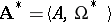 for which
for which 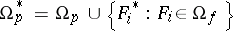 . Submodels of the model
. Submodels of the model 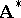 are called submodels of the
are called submodels of the  -system
-system 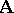 . For any non-empty finite subsets
. For any non-empty finite subsets 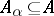 ,
, 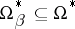 , the model
, the model  is called a finite depletion of the finite submodel
is called a finite depletion of the finite submodel 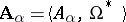 of the
of the  -system
-system 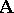 . An
. An  -system
-system 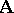 is said to be locally imbeddable in a class
is said to be locally imbeddable in a class 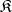 of
of  -systems if for each finite depletion
-systems if for each finite depletion 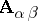 of any finite submodel
of any finite submodel 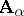 of the
of the  -system
-system 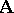 there exists in the class
there exists in the class 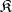 an
an  -system
-system 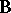 (depending on the chosen finite depletion
(depending on the chosen finite depletion 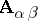 ) such that the model
) such that the model 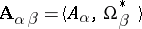 is isomorphic to the model
is isomorphic to the model  for a suitable subset
for a suitable subset 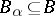 .
.
A subclass 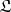 of a class
of a class 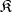 of
of  -systems is called universal (or universally axiomatizable) in
-systems is called universal (or universally axiomatizable) in 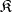 if there exists a set
if there exists a set 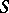 of universal formulas of the signature
of universal formulas of the signature  such that
such that  .
.
The Tarski–Los theorem: A subclass 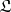 of a class
of a class 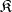 of
of  -systems is universal in
-systems is universal in 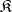 if and only if
if and only if 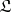 contains all systems from
contains all systems from 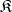 which are locally imbeddable in
which are locally imbeddable in 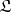 .
.
Filtered products.
Let 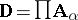 be the Cartesian product of the
be the Cartesian product of the  -systems
-systems 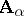 (
(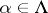 ,
,  ) and let
) and let 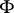 be some filter over
be some filter over 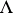 . The relation
. The relation
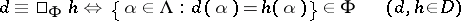 |
is an equivalence relation on the underlying set 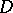 of the
of the  -system
-system 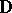 . For each element
. For each element 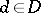 , let
, let 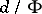 be the coset by this equivalence and let
be the coset by this equivalence and let 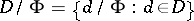 . Putting
. Putting
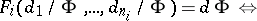 |
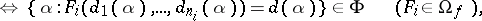 |
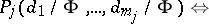 |
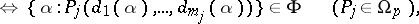 |
one obtains the  -system
-system 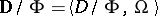 , which is called the product of the
, which is called the product of the  -systems
-systems 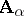 (
( ) filtered through the filter
) filtered through the filter 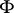 . The
. The  -systems
-systems 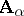 (
(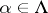 ) are said to be the factors of this product. If
) are said to be the factors of this product. If 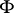 is an ultrafilter over
is an ultrafilter over 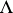 , the filtered product
, the filtered product 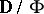 is known as the ultraproduct of the
is known as the ultraproduct of the  -systems
-systems 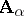 (
(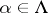 ).
).
The ultraproduct theorem: If 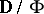 is the ultraproduct of the
is the ultraproduct of the  -systems
-systems 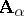 (
(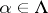 ) and if
) and if 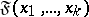 is an arbitrary formula of the signature
is an arbitrary formula of the signature  in which
in which  are free object variables, then for any elements
are free object variables, then for any elements 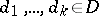 :
:
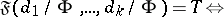 |
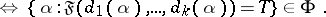 |
In particular, a closed formula  of the signature
of the signature  is true in the ultraproduct
is true in the ultraproduct 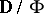 of the
of the  -systems
-systems 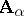 (
(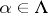 ) if and only if the set of numbers of factors in which the formula
) if and only if the set of numbers of factors in which the formula 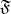 is true belongs to the ultrafilter
is true belongs to the ultrafilter 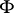 . Therefore, any axiomatizable class of
. Therefore, any axiomatizable class of  -systems is closed with respect to ultraproducts.
-systems is closed with respect to ultraproducts.
A class 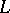 of
of  -systems is universally axiomatizable if and only if it is closed with respect to subsystems and ultraproducts.
-systems is universally axiomatizable if and only if it is closed with respect to subsystems and ultraproducts.
An  -system
-system 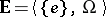 is said to be a unit if its underlying set consists of a single element, e.g. an element
is said to be a unit if its underlying set consists of a single element, e.g. an element  , and if
, and if 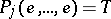 for all
for all 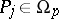 .
.
Mal'tsev's theorem: A class 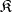 of
of  -systems is a quasi-variety if and only if it contains a unit
-systems is a quasi-variety if and only if it contains a unit  -system and is closed with respect to subsystems and filtered products (through an arbitrary filter).
-system and is closed with respect to subsystems and filtered products (through an arbitrary filter).
Completeness and categoricity.
A non-empty class 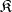 of
of  -systems is called categorical if all
-systems is called categorical if all  -systems from
-systems from 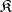 are mutually isomorphic. Any categorical axiomatizable class of
are mutually isomorphic. Any categorical axiomatizable class of  -systems consists of one (up to an isomorphism) finite
-systems consists of one (up to an isomorphism) finite  -system.
-system.
A class 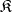 of
of  -systems is called categorical in cardinality
-systems is called categorical in cardinality 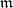 if it contains an
if it contains an  -system of cardinality
-system of cardinality 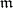 and if all
and if all  -systems from
-systems from 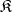 of cardinality
of cardinality 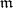 are mutually isomorphic. For example, the class of algebraically closed fields of fixed characteristic is categorical in any uncountable infinite cardinality. A non-empty class
are mutually isomorphic. For example, the class of algebraically closed fields of fixed characteristic is categorical in any uncountable infinite cardinality. A non-empty class 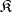 of
of  -systems is called complete if for any
-systems is called complete if for any  -systems
-systems 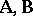 from
from 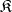 the equality
the equality  is valid.
is valid.
Vaught's theorem. If an axiomatizable class 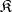 of
of  -systems is categorical in some cardinality
-systems is categorical in some cardinality 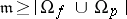 and if all
and if all  -systems in
-systems in 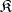 are infinite, then
are infinite, then 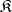 is a complete class.
is a complete class.
In particular, the class of all algebraically closed fields of fixed characteristic is complete.
See also Algebraic system, automorphism of an; Algebraic systems, quasi-variety of; Algebraic systems, class of; Algebraic systems, variety of.
References
| [1] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
| [2] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [3] | G. Grätzer, "Universal algebra" , Springer (1979) |
| [4] | J.L. Bell, A.B. Slomson, "Models and ultraproducts: an introduction" , North-Holland (1971) |
| [5] | C.C. Chang, H.J. Keisler, "Model theory" , North-Holland (1973) |
Comments
The terminology in use for this subject in English-speaking countries differs in a number of respects from the Russian terminology. What is here called an algebraic system is usually called a (first-order) structure (a structure of type  , if a given signature or similarity type
, if a given signature or similarity type  has been specified); the term algebra is often used instead of "structure" in the case when
has been specified); the term algebra is often used instead of "structure" in the case when  has no primitive relations. The term model is reserved for a structure which satisfies a given set of first-order sentences (closed formulas); it is not normally used in the sense defined above. The underlying set of a structure is sometimes called its universe.
has no primitive relations. The term model is reserved for a structure which satisfies a given set of first-order sentences (closed formulas); it is not normally used in the sense defined above. The underlying set of a structure is sometimes called its universe.
Although the text is correct in saying that the subject was largely developed in the 1950s (principally through work of L.A. Henkin [L.A. Khenkin], A.I. Mal'tsev, A. Robinson and A. Tarski), two important precursors dating from 1935 should be mentioned. They are Birkhoff's theorem characterizing varieties of algebras [a1] and Tarski's definition of validity of formulas in a first-order structure [a2].
References
| [a1] | G. Birkhoff, "On the structure of abstract algebras" Proc. Cambridge Philos. Soc. , 31 (1935) pp. 433–454 |
| [a2] | A. Tarski, "Der Wahrheitsbegriff in den formalisierten Sprachen" Studia Philos. , 1 (1935) pp. 261–405 |
Algebraic system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_system&oldid=12791