Potential field
gradient field
The vector field generated by the gradients of a scalar function 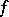 in several variables
in several variables 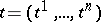 which belong to some domain
which belong to some domain 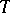 in an
in an  -dimensional space. The function
-dimensional space. The function 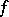 is called the scalar potential (potential function) of this field. A potential field is completely integrable over
is called the scalar potential (potential function) of this field. A potential field is completely integrable over 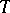 : The Pfaffian equation
: The Pfaffian equation 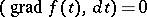 has the level lines
has the level lines  or the level surfaces
or the level surfaces 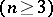 of the potential
of the potential 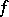 as
as 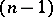 -dimensional integral manifolds. Any regular covariant field
-dimensional integral manifolds. Any regular covariant field  that is completely integrable over
that is completely integrable over 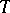 is obtained by multiplying the potential field by a scalar:
is obtained by multiplying the potential field by a scalar:
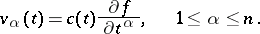 |
The scalar 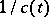 is called an integrating factor of the Pfaffian equation
is called an integrating factor of the Pfaffian equation 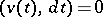 . The following equalities serve as a test for the field
. The following equalities serve as a test for the field  to be the gradient of a potential (
to be the gradient of a potential (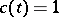 ):
):
 |
They indicate that the field 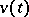 is rotation free (see Curl).
is rotation free (see Curl).
The concept of a potential field is widely used in mechanics and physics. The majority of force fields and electric fields can be considered as potential fields. For instance, if 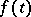 is the pressure at a point
is the pressure at a point 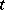 of an ideal fluid filling a region
of an ideal fluid filling a region 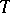 , then the vector
, then the vector  is equal to the equilibrium pressure force applied to the volume element
is equal to the equilibrium pressure force applied to the volume element 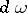 . If
. If  is the temperature of a heated body
is the temperature of a heated body 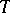 at a point
at a point 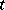 , then the vector
, then the vector 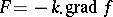 , where
, where 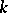 is the thermal conductivity coefficient, is equal to the density of the heat flow in the direction of less heated parts of the body (in the direction orthogonal to the isothermal surfaces
is the thermal conductivity coefficient, is equal to the density of the heat flow in the direction of less heated parts of the body (in the direction orthogonal to the isothermal surfaces 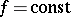 ).
).
Comments
In the above, complete integrability of a vector field 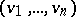 means that the Pfaffian equation
means that the Pfaffian equation 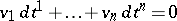 defines an involutive distribution, i.e. an integrable one. A differential
defines an involutive distribution, i.e. an integrable one. A differential 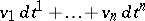 such that
such that 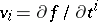 for some potential
for some potential 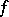 is called a total differential and the corresponding function
is called a total differential and the corresponding function 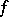 is sometimes called a complete integral. Especially for
is sometimes called a complete integral. Especially for 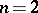 ,
, 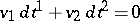 is called an exact differential equation.
is called an exact differential equation.
References
| [a1] | H. Triebel, "Analysis and mathematical physics" , Reidel (1986) pp. Sect. 10.1.4 |
| [a2] | E. Zauderer, "Partial differential equations" , Wiley (Interscience) (1989) pp. 92 |
| [a3] | K. Rektorys (ed.) , Applicable mathematics , Iliffe (1969) pp. Sects. 12.3, 14.7 |
Potential field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_field&oldid=12775