Ordered ring
partially ordered ring
A ring  (not necessarily associative) which is a partially ordered group under addition and in which for any elements
(not necessarily associative) which is a partially ordered group under addition and in which for any elements  the inequalities
the inequalities  and
and  imply
imply  and
and  . Every ring is an ordered ring for the trivial order. As examples of ordered rings one may take an ordered field; the ring of real functions on a set
. Every ring is an ordered ring for the trivial order. As examples of ordered rings one may take an ordered field; the ring of real functions on a set  , where
, where  means that
means that  for all
for all 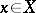 ; or a matrix ring over an ordered ring
; or a matrix ring over an ordered ring 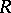 , where, by definition,
, where, by definition,  if
if 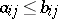 for all
for all 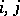 . If
. If 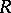 is an ordered ring, then the set
is an ordered ring, then the set
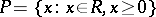 |
is called its positive cone. The positive cone of an ordered ring completely defines the order: 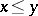 if and only if
if and only if 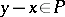 . A subset
. A subset 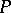 of a ring
of a ring 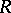 can serve as the positive cone for some order if and only if
can serve as the positive cone for some order if and only if
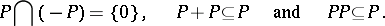 |
The equation 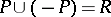 is equivalent to the totality of the order (cf. Totally ordered set).
is equivalent to the totality of the order (cf. Totally ordered set).
An ordered ring that is totally ordered or lattice-ordered is accordingly called a totally ordered or lattice-ordered ring (cf. also Archimedean ring). Lattice-ordered rings turn out to be distributive lattices, and their additive groups are torsion-free (cf. Lattice-ordered group). Certain questions in the theory of associative rings and, in particular, in the theory of radicals have analogues in associative lattice-ordered rings. The class of rings which allow a lattice-ordered ring structure is not axiomatizable. If 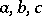 are elements of a lattice-ordered ring and
are elements of a lattice-ordered ring and 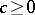 , then the following relations hold:
, then the following relations hold:
 |
 |
Ideals in lattice-ordered rings which are convex subgroups (cf. Convex subgroup) of the additive group are called  -ideals. The quotient ring by an
-ideals. The quotient ring by an 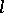 -ideal can be made into a lattice-ordered ring in a natural way. The homomorphism theorem holds.
-ideal can be made into a lattice-ordered ring in a natural way. The homomorphism theorem holds.
A lattice-ordered ring 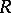 is called a functional ring or an
is called a functional ring or an 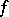 -ring if it satisfies any of the following equivalent conditions: 1)
-ring if it satisfies any of the following equivalent conditions: 1) 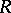 is isomorphic to a lattice-ordered subring of a direct product of totally ordered rings; 2) for any
is isomorphic to a lattice-ordered subring of a direct product of totally ordered rings; 2) for any  one has the implication
one has the implication
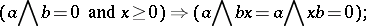 |
3) for any subset 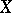 of
of  the set
the set
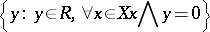 |
is an 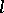 -ideal; and 4) for any
-ideal; and 4) for any 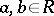 ,
,
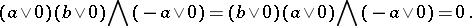 |
Condition 4) shows that  -rings form a variety of signature
-rings form a variety of signature 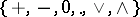 . Neither of the equations in this condition is a consequence of the other. Not every
. Neither of the equations in this condition is a consequence of the other. Not every 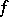 -ring can be imbedded in an
-ring can be imbedded in an 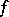 -ring with a unit element. If
-ring with a unit element. If 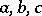 are elements of an
are elements of an  -ring and
-ring and 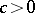 , then one has
, then one has
 |
 |
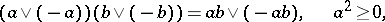 |
as well as the implication 
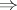
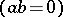 .
.
An order of an ordered ring 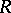 with a positive cone
with a positive cone 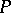 can be extended to a total order such that
can be extended to a total order such that 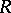 becomes a totally ordered ring if and only if for any finite set
becomes a totally ordered ring if and only if for any finite set  in
in 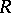 one can choose
one can choose  or
or  such that in the semi-ring generated by
such that in the semi-ring generated by 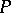 and the elements
and the elements  the sum of any two non-zero elements is non-zero. With
the sum of any two non-zero elements is non-zero. With 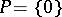 one obtains a criterion for the possibility of having a total order on the ring.
one obtains a criterion for the possibility of having a total order on the ring.
References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [2] | A.A. Vinogradov, "The non-axiomatizability of lattice-ordered rings" Math. Notes , 21 (1977) pp. 253–254 Mat. Zametki , 21 : 4 (1977) pp. 449–452 |
| [3] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
| [4] | A. Bigard, K. Keimel, S. Wolfenstein, "Groupes et anneaux reticulés" , Springer (1977) |
| [5] | G.W. Brumfiel, "Partially ordered rings and semi-algebraic geometry" , Cambridge Univ. Press (1979) |
| [6] | S.A. Steinberg, "Radical theory in lattice-ordered rings" Symp. Mat. Ist. Naz. Alta Mat. , 21 (1977) pp. 379–400 |
| [7] | S.A. Steinberg, "Examples of lattice-ordered rings" J. of Algebra , 72 : 1 (1981) pp. 223–236 |
Comments
For a survey of the current state-of-the-art in the field see the second part of [a1].
References
| [a1] | J. Martinez (ed.) , Ordered algebraic structures , Kluwer (1989) |
Ordered ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ordered_ring&oldid=12730