Haken manifold

sufficiently-large -manifold, sufficiently-large three-dimensional manifold

A compact, 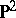-irreducible three-dimensional manifold which contains a properly embedded, incompressible, two-sided surface.

All objects and mappings are in the piecewise-linear category (cf. also Piecewise-linear topology). The surface 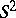denotes the two-dimensional sphere, while 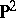denotes the projective plane. A surface 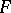properly embedded in a three-dimensional manifold 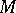is two-sided in 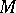if it separates its regular neighbourhood in 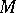. A three-dimensional manifold 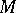is reducible (reducible with respect to connected sum decomposition) if it contains a properly embedded two-dimensional sphere that does not bound a three-dimensional cell in . Otherwise, the three-dimensional manifold 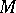is irreducible. If the three-dimensional manifold 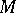is irreducible and does not contain an embedded, two-sided 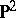, it is said to be 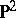-irreducible. An orientable three-dimensional manifold is 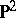-irreducible if it is irreducible. A surface 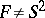which is properly embedded in a three-dimensional manifold 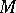is compressible in 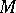if there is a disc 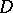embedded in 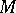such that 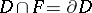and the simple closed curve 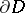does not bound a disc in 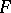. Otherwise, such a surface 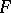is said to be incompressible in 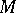. For two-sided surfaces it follows from the Dehn lemma that this geometric condition is equivalent to the inclusion mapping of fundamental groups, 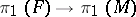, being injective.

The three-dimensional cell is a Haken manifold, as is any compact, 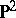-irreducible three-dimensional manifold with non-empty boundary. In fact, a sufficient condition for a compact, 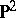-irreducible three-dimensional manifold 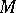to be a Haken manifold is that its first homology group with rational coefficients, 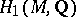, be non-zero. This condition is not necessary. Any closed three-dimensional manifold which is not a Haken manifold is said to be a non-Haken manifold. It is conjectured that every closed, 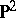-irreducible three-dimensional manifold with infinite fundamental group has a finite sheeted covering space (cf. also Covering surface) that is a Haken manifold.

An embedded, incompressible surface in a three-dimensional manifold is a very useful tool. However, in the case of three-dimensional manifolds with non-empty boundary, it is necessary to add an additional condition related to the boundary to achieve the same geometric character of the incompressible surface in a closed three-dimensional manifold. 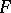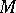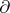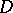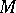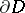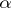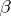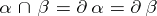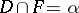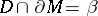A properly embedded surface in a three-dimensional manifold with non-empty boundary is boundary compressible, written -compressible, if there is a disc embedded in such that is the union of two arcs and , , , , and does not cobound a disc in 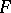with an arc in . If a properly embedded surface in a three-dimensional manifold 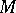is not 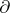-compressible, it is said to be boundary incompressible (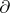-incompressible). There is an algebraic interpretation of this geometric condition in terms of relative fundamental groups analogous to that given above in the case of an incompressible surface. Any compact, 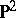-irreducible three-dimensional manifold 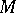with non-empty boundary, other than the three-dimensional cell, contains a properly embedded, incompressible and 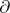-incompressible surface that is not a disc parallel into .

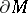Just as two-dimensional manifolds have families of embedded simple closed curves that split them into more simple pieces, the existence of incompressible and 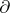-incompressible surfaces in Haken manifolds allow them to be split into more simple pieces. If 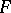is a properly embedded, two-sided surface in a three-dimensional manifol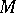d and 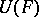is the interior of some regular neighbourhood of 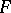in 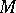, then 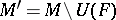is the three-dimensional manifold obtained by splitting 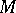at 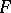. A partial hierarchy for 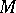is a finite or infinite sequence of manifold pairs

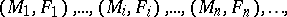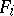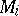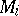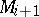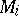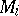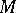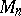where is a properly embedded, two-sided, incompressible surface in which is not parallel into the boundary of , and is obtained from by splitting at . A partial hierarchy is said to be a hierarchy for if for some , each component of is a a three-dimensional cell. Necessarily, a hierarchy for 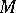is a finite partial hierarchy, 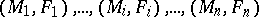, and is called the length of the hierarchy.

The fundamental theorem for Haken manifolds is that every Haken manifold has a hierarchy, 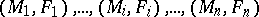, where each 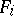is incompressible and 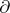-incompressible in 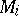. The existence of a hierarchy admits inductive methods of analysis and proof. This is exhibited in many of the major results regarding three-dimensional manifolds. For example, the problem of determining if two given three-dimensional manifolds are homeomorphic (the homeomorphism problem), the problem of determining if a given loop in a three-dimensional manifold is contractible (the word problem), and the problem of determining if a closed, orientable, irreducible, atoroidal (having no embedded, incompressible tori) three-dimensional manifold admits a metric with constant negative curvature, (uniformization), have all been solved for Haken manifolds but remain open (as of 2000) for closed, orientable, irreducible three-dimensional manifolds in general. The study of Haken manifolds is quite rich and includes a large part of the knowledge and understanding of three-dimensional manifolds.

References

[a1]	W. Haken, "Theorie der Normal Flächen I" Acta Math. , 105 (1961) pp. 245–375
[a2]	F. Waldhausen, "On irreducible -manifolds which are sufficiently large" Ann. of Math. , 87 (1968) pp. 56–88
[a3]	W. Thurston, "Three-dimensional manifolds, Kleinian groups and hyperbolic geometry" Bull. Amer. Math. Soc. (N.S.) , 6 (1982) pp. 357–381
[a4]	F. Waldhausen, "The word problem in fundamental groups of sufficiently large irreducible 3-manifolds" Ann. of Math. , 88 (1968) pp. 272–280
[a5]	A.T. Fomenko, S.V. Matveev, "Algorithmic and computer methods for three-manifolds" , Kluwer Acad. Publ. (1997)