Lie group, local
local analytic group
An analytic manifold 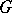 over a field
over a field 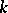 that is complete with respect to some non-trivial absolute value, which is endowed with a distinguished element
that is complete with respect to some non-trivial absolute value, which is endowed with a distinguished element  (the identity), an open subset
(the identity), an open subset 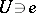 and a pair of analytic mappings
and a pair of analytic mappings 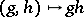 of the manifold
of the manifold 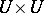 into
into 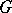 and
and 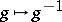 of the neighbourhood
of the neighbourhood 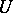 into itself, for which:
into itself, for which:
1) in some neighbourhood of  one has
one has 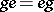 ;
;
2) in some neighbourhood of  one has
one has 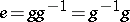 ;
;
3) for some neighbourhood 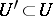 of
of  one has
one has 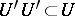 and
and 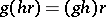 , where
, where 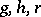 are arbitrary elements of
are arbitrary elements of 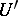 .
.
Local Lie groups first made their appearance in the work of S. Lie and his school (see [1]) as local Lie transformation groups (cf. Lie transformation group).
Let 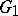 and
and 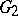 be two local Lie groups with identities
be two local Lie groups with identities 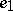 and
and 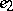 , respectively. A local homomorphism of
, respectively. A local homomorphism of 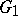 into
into 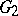 (denoted by
(denoted by  ) is an analytic mapping
) is an analytic mapping 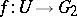 of some neighbourhood
of some neighbourhood 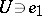 in
in 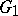 for which
for which 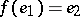 and
and 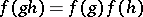 for
for 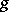 and
and 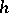 in some neighbourhood
in some neighbourhood 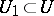 of
of 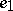 . The naturally defined composition of local homomorphisms is also a local homomorphism. Local homomorphisms
. The naturally defined composition of local homomorphisms is also a local homomorphism. Local homomorphisms 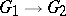 that coincide in some neighbourhood of
that coincide in some neighbourhood of 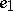 are said to be equivalent. If there are local homomorphism
are said to be equivalent. If there are local homomorphism 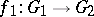 and
and 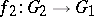 such that the compositions
such that the compositions  and
and 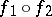 are equivalent to the identity mappings, then the local Lie groups
are equivalent to the identity mappings, then the local Lie groups 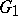 and
and 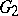 are said to be equivalent.
are said to be equivalent.
Examples. Let 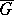 be an analytic group with identity
be an analytic group with identity  and
and 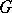 an open neighbourhood of
an open neighbourhood of  in
in 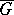 . Then the analytic structure on
. Then the analytic structure on 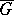 induces an analytic structure on
induces an analytic structure on 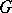 , and the operations of multiplication and taking the inverse of an element in
, and the operations of multiplication and taking the inverse of an element in 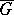 convert
convert 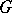 into a local Lie group (in particular,
into a local Lie group (in particular, 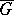 itself can be regarded as a local Lie group). All local Lie groups
itself can be regarded as a local Lie group). All local Lie groups 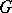 obtainable in this way from a fixed analytic group
obtainable in this way from a fixed analytic group 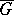 are equivalent to one another.
are equivalent to one another.
One of the fundamental questions in the theory of Lie groups is the question of how general a character the example given above has, that is, whether every local Lie group is (up to equivalence) a neighbourhood of some analytic group. The answer to this question is affirmative (see [2], [3], [4]; in the case of local Banach Lie groups the answer is negative, see [4]).
The most important tool for studying local Lie groups is the correspondence between the local Lie group and its Lie algebra. Namely, let 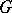 be a local Lie group over a field
be a local Lie group over a field 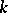 and let
and let  be the identity of it. The choice of a chart
be the identity of it. The choice of a chart  of the analytic manifold
of the analytic manifold 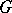 at the point
at the point  makes it possible to identify some neighbourhood of
makes it possible to identify some neighbourhood of  in
in 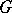 with some neighbourhood
with some neighbourhood 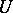 of the origin in the
of the origin in the  -dimensional coordinate space
-dimensional coordinate space 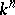 , so that
, so that 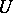 becomes a local Lie group. Let
becomes a local Lie group. Let 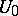 be a neighbourhood of the origin in the local Lie group
be a neighbourhood of the origin in the local Lie group 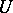 such that for any
such that for any 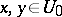 a product
a product 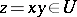 is defined. Then, in coordinate form, multiplication in
is defined. Then, in coordinate form, multiplication in 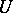 in the neighbourhood
in the neighbourhood 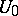 is specified by
is specified by  analytic functions
analytic functions
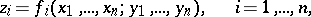 |
where 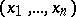 ,
, 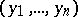 ,
, 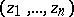 are, respectively, the coordinates of the points
are, respectively, the coordinates of the points 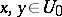 and
and 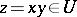 . In a sufficiently small neighbourhood of the origin the function
. In a sufficiently small neighbourhood of the origin the function 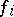 is represented as the sum of a convergent power series (also denoted by
is represented as the sum of a convergent power series (also denoted by 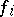 henceforth), and the presence in
henceforth), and the presence in 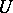 of an identity and the associative law is expressed by the following properties of these series, regarded as formal power series in
of an identity and the associative law is expressed by the following properties of these series, regarded as formal power series in 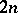 variables:
variables:
a) 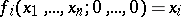 and
and 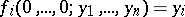 for all
for all 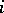 ;
;
b) 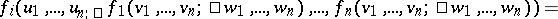
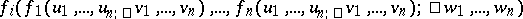 for all
for all 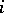 .
.
Properties a) and b) imply that the system of formal power series 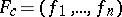 is a formal group. In particular, the homogeneous component of degree 2 of each of the series
is a formal group. In particular, the homogeneous component of degree 2 of each of the series 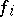 is a bilinear form on
is a bilinear form on 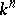 , that is, it has the form
, that is, it has the form
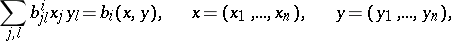 |
which makes it possible to define a multiplication  on
on 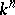 according to the rule:
according to the rule:
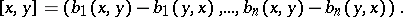 |
With respect to this multiplication 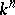 is a Lie algebra. The structure of a Lie algebra carries over to the tangent space
is a Lie algebra. The structure of a Lie algebra carries over to the tangent space 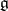 to
to  at
at  by means of the chart
by means of the chart  , defined above, by the isomorphism
, defined above, by the isomorphism 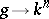 . The formal groups
. The formal groups 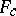 and
and 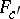 defined by different charts are isomorphic, and the structure of a Lie algebra on
defined by different charts are isomorphic, and the structure of a Lie algebra on 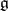 does not depend on the choice of the chart
does not depend on the choice of the chart  . The Lie algebra
. The Lie algebra 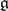 is called the Lie algebra of a local Lie group. For any local homomorphism of a local Lie group its differential at the identity is a homomorphism of Lie algebras, which implies that the correspondence between a local Lie group and its Lie algebra is functorial. In particular, equivalent local Lie groups have isomorphic Lie algebras.
is called the Lie algebra of a local Lie group. For any local homomorphism of a local Lie group its differential at the identity is a homomorphism of Lie algebras, which implies that the correspondence between a local Lie group and its Lie algebra is functorial. In particular, equivalent local Lie groups have isomorphic Lie algebras.
If the field 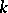 has characteristic 0, then the construction given above, which goes back to Lie [1], makes it possible to reduce the study of properties of local Lie groups to the study of the corresponding properties of their Lie algebras. In this case the Lie algebra
has characteristic 0, then the construction given above, which goes back to Lie [1], makes it possible to reduce the study of properties of local Lie groups to the study of the corresponding properties of their Lie algebras. In this case the Lie algebra 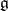 determines the local Lie group
determines the local Lie group 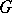 uniquely up to equivalence. Namely, the chart
uniquely up to equivalence. Namely, the chart  can be chosen so that the product
can be chosen so that the product 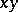 in the local Lie group
in the local Lie group 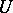 is expressed as a convergent series (the so-called Campbell–Hausdorff series) of elements of
is expressed as a convergent series (the so-called Campbell–Hausdorff series) of elements of 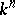 obtained from
obtained from  and
and 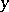 by means of the commutation operation
by means of the commutation operation 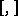 and multiplication by elements of
and multiplication by elements of 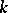 (see Campbell–Hausdorff formula). Conversely, for an arbitrary finite-dimensional Lie algebra
(see Campbell–Hausdorff formula). Conversely, for an arbitrary finite-dimensional Lie algebra 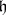 over
over 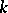 the Campbell–Hausdorff series converges in some neighbourhood of the origin in
the Campbell–Hausdorff series converges in some neighbourhood of the origin in 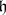 and determines in this neighbourhood the structure of a local Lie group with Lie algebra
and determines in this neighbourhood the structure of a local Lie group with Lie algebra 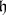 . Thus, for any given Lie algebra
. Thus, for any given Lie algebra 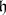 there is a unique (up to equivalence) local Lie group with
there is a unique (up to equivalence) local Lie group with 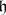 as its Lie algebra. Moreover, every homomorphism of Lie algebras is induced by a unique homomorphism of the corresponding local Lie groups. In other words, the correspondence between a local Lie group and its Lie algebra defines an equivalence of the category of local Lie groups and the category of finite-dimensional Lie algebras over
as its Lie algebra. Moreover, every homomorphism of Lie algebras is induced by a unique homomorphism of the corresponding local Lie groups. In other words, the correspondence between a local Lie group and its Lie algebra defines an equivalence of the category of local Lie groups and the category of finite-dimensional Lie algebras over 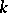 . Moreover, the correspondence between a local Lie group and the corresponding formal group defines an equivalence of the category of local Lie groups and the category of formal groups over
. Moreover, the correspondence between a local Lie group and the corresponding formal group defines an equivalence of the category of local Lie groups and the category of formal groups over 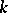 .
.
The Lie algebra can also be defined for any local Banach Lie group; the main result about the equivalence of the categories of local Lie groups and Lie algebras can be generalized to this case (see [2]).
References
| [1] | S. Lie, F. Engel, "Theorie der Transformationsgruppen" , 1–3 , Leipzig (1888–1893) |
| [2] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [3] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [4] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [5] | N.G. Chebotarev, "The theory of Lie groups" , Moscow-Leningrad (1940) (In Russian) |
Comments
The equivalences of categories between local Lie groups, formal groups and Lie algebras over a field 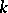 only hold for fields
only hold for fields  of characteristic zero. In particular, for a field
of characteristic zero. In particular, for a field 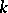 of characteristic
of characteristic 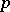 there are at least countably many non-isomorphic
there are at least countably many non-isomorphic 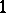 -dimensional formal groups over
-dimensional formal groups over 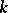 , while there is of course only one
, while there is of course only one 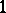 -dimensional Lie algebra over
-dimensional Lie algebra over 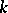 .
.
Lie group, local. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_group,_local&oldid=12719