Categoric system of axioms

categorical system of axioms

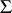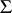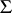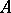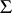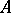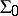Any system of axioms for which all models of the signature of satisfying these axioms are isomorphic. It follows from the Mal'tsev–Tarski theorem on elementary extensions that models of a categorical first-order system of axioms have finite cardinality. The converse also holds: For any finite model there exists a categorical first-order system of axioms whose models are isomorphic to . Let be the set of universal closures of the formulas

1) ;

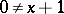2) ;

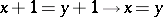3) ;

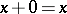4) ;

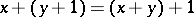5) ;

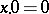6) ;

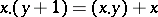7) 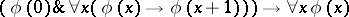, where 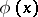is any formula of signature .

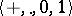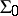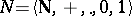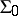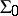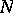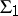This system of axioms is known under the name of Peano arithmetic. The model of natural numbers is a model for . However, there exists a model of that is not isomorphic to . Let be the system obtained from 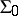by replacing the scheme of elementary induction 7) by the axiom of complete induction

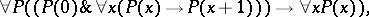written in a second-order language. Then the system 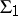is categorical and all models of 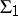are isomorphic to 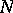. Another method of categorical description of 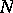consists in appending to 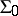the following infinite axiom (of the language ):

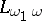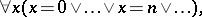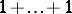when is short for the sum of ones.

References

[1]	J.R. Shoenfield, "Mathematical logic" , Addison-Wesley (1967)