Absorbing state
of a Markov chain 
A state  such that
such that
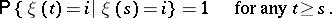 |
An example of a Markov chain with absorbing state  is a branching process.
is a branching process.
The introduction of additional absorbing states is a convenient technique that enables one to examine the properties of trajectories of a Markov chain that are associated with hitting some set.
Example. Consider the set  of states of a homogeneous Markov chain
of states of a homogeneous Markov chain  with discrete time and transition probabilities
with discrete time and transition probabilities
 |
in which a subset  is distinguished and suppose one has to find the probabilities
is distinguished and suppose one has to find the probabilities
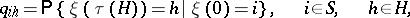 |
where 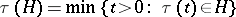 is the moment of first hitting the set
is the moment of first hitting the set  . If one introduces the auxiliary Markov chain
. If one introduces the auxiliary Markov chain 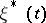 differing from
differing from 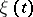 only in that all states
only in that all states 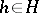 are absorbing in
are absorbing in 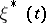 , then for
, then for 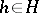 the probabilities
the probabilities
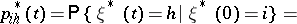 |
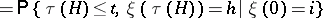 |
are monotonically non-decreasing for 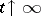 and
and
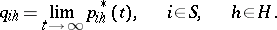 | (*) |
By virtue of the basic definition of a Markov chain
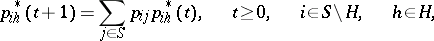 |
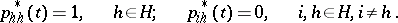 |
The passage to the limit for 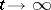 taking into account (*) gives a system of linear equations for
taking into account (*) gives a system of linear equations for 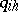 :
:
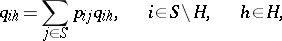 |
 |
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1968) |
Absorbing state. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Absorbing_state&oldid=12666