Congruence (in algebra)
An equivalence relation 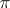 on a universal algebra
on a universal algebra 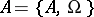 commuting with all operations in
commuting with all operations in  , that is, an equivalence relation such that
, that is, an equivalence relation such that 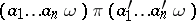 whenever
whenever 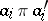 , where
, where  ,
, 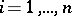 , and
, and 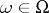 is an
is an  -ary operation. Congruences in algebraic systems are defined in a similar way. Thus, the equivalence classes modulo a congruence
-ary operation. Congruences in algebraic systems are defined in a similar way. Thus, the equivalence classes modulo a congruence 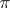 form a universal algebra (algebraic system)
form a universal algebra (algebraic system)  of the same type as
of the same type as 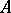 , called the quotient algebra (or quotient system) modulo
, called the quotient algebra (or quotient system) modulo 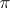 . The natural mapping from
. The natural mapping from 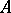 onto
onto 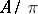 (which takes an element
(which takes an element  to the
to the  -class containing it) is a surjective homomorphism. Conversely, every homomorphism
-class containing it) is a surjective homomorphism. Conversely, every homomorphism 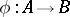 defines a unique congruence, whose classes are the pre-images of the elements of
defines a unique congruence, whose classes are the pre-images of the elements of 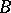 .
.
The intersection of a family of congruences 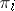 ,
, 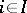 , in the lattice of relations on a universal algebra (algebraic system) is a congruence. In general, a union of congruences in the lattice of relations is not a congruence. The product
, in the lattice of relations on a universal algebra (algebraic system) is a congruence. In general, a union of congruences in the lattice of relations is not a congruence. The product  of two congruences
of two congruences 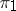 and
and 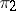 is a congruence if and only if
is a congruence if and only if 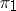 and
and 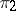 commute, i.e. if and only if
commute, i.e. if and only if 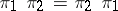 .
.
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
Comments
References
| [a1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
Congruence (in algebra). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Congruence_(in_algebra)&oldid=12653