Unconditional summability

Summability of a series for all possible rearrangements of its terms. The series

(*)

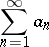is called unconditionally summable by some summation method (unconditionally -summable) if it is summable by this method to a sum whatever the ordering of its terms, where the value of may depend on the particular rearrangement (cf. Summation methods). The study of unconditional summability originated with W. Orlicz [1]; he showed, in particular, that if , then absolute summability of the series by a linear regular method (cf. Regular summation methods) implies unconditional convergence. It was subsequently shown that this condition may be replaced by a weaker one: [2]. Unconditional summability by a matrix method does not imply unconditional convergence; in fact, take the series . If is a regular matrix summation method and if the series (*) is unconditionally 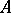-summable, then all its terms have the form 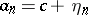, where is a constant and the series with terms is absolutely convergent: ; moreover, 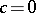if the method 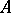does not sum the series 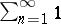[3].

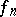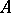In the case of series of functions one distinguishes between summability in measure, everywhere summability, almost-everywhere summability, etc. 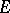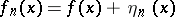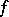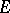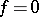For unconditional summability of a series of functions, the following statement is valid almost-everywhere: If the series of measurable functions on a set is unconditionally -summable almost-everywhere on , then the terms of this series have the form , where is a finite measurable function on and the series is unconditionally almost-everywhere convergent on ; also, if 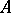does not sum [2].

References

[1]	W. Orlicz, Bull. Acad. Polon. Sci. Sér. Sci. Math., Astr. Phys. : 3A (1927) pp. 117–125
[2]	P.L. Ul'yanov, "Unconditional summability" Izv. Akad. Nauk SSSR Ser. Mat. , 23 (1959) pp. 781–808 (In Russian)
[3]	V.F. Gaposhkin, A.M. Olevskii, Nauchn. Dokl. Vyssh. Shkoly Fiz.-Mat. Nauk. , 6 (1958) pp. 81–86

References

[a1]	K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970)