Fundamental class

The fundamental class of an -connected topological space (that is, a topological space such that for ) is the element of the group that corresponds, under the isomorphism that arises in the universal coefficient formula

to the inverse 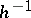of the Hurewicz homomorphism 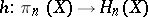(which is an isomorphism by the Hurewicz theorem (see Homotopy group)). If 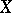is a CW-complex (a cellular space), then the fundamental class 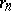is the same as the first obstruction to the construction of a section of the Serre fibration 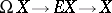, which lies in 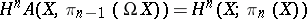, and also as the first obstruction to the construction of a homotopy of the identity mapping 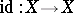to a constant mapping. In case the 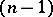-dimensional skeleton of 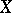consists of a single point (in fact this assumption involves no loss of generality, since any 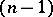-dimensional CW-complex is homotopy equivalent to a CW-complex without cells of positive dimension less than ), the closure of each -dimensional cell is an -dimensional sphere, and so its characteristic mapping determines some element of the group 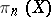. Since these cells form a basis of the group 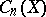, it thus determines an -dimensional cochain in 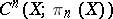. This cochain is a cocycle and its cohomology class is also the fundamental class.

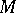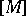A fundamental class, or orientation class, of a connected oriented -dimensional manifold without boundary (respectively, with boundary ) is a generator of the group 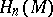(respectively, of 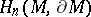), which is a free cyclic group. If 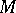can be triangulated, then the fundamental class is the homology class of the cycle that is the sum of all coherent oriented -dimensional simplices of an arbitrary triangulation of it. For each 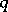, the homomorphism

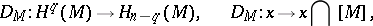where the 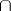-product is defined by the formula

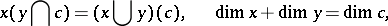is an isomorphism, called Poincaré duality (if has boundary 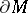, then 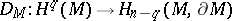). One also speaks of the fundamental class for non-oriented (but connected) manifolds 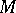(with boundary); in this case one means by it the unique element of 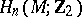(respectively, of 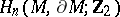) different from zero. In this case there is also a Poincaré duality.

References

[1]	D.B. Fuks, A.T. Fomenko, V.L. Gutenmakher, "Homotopic topology" , Moscow (1969) (In Russian)
[2]	R.E. Mosher, M.C. Tangora, "Cohomology operations and applications in homotopy theory" , Harper & Row (1968)
[3]	D. Husemoller, "Fibre bundles" , McGraw-Hill (1966)
[4]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966)
[5]	A. Dold, "Lectures on algebraic topology" , Springer (1980)