Classical group
The group of automorphisms of some sesquilinear form 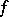 on a right
on a right 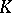 -module
-module 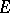 , where
, where 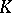 is a ring; here
is a ring; here 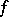 and
and 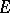 (and sometimes
(and sometimes 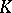 as well) usually satisfy extra conditions. There is no precise definition of a classical group. It is supposed that
as well) usually satisfy extra conditions. There is no precise definition of a classical group. It is supposed that 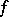 is either the null form or is a non-degenerate reflexive form; sometimes
is either the null form or is a non-degenerate reflexive form; sometimes 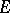 is taken to be a free module of finite type. Often one means by classical groups other groups closely related to groups of automorphisms of forms (for example, their commutator subgroups or quotients with respect to the centre) or some of their extensions (for example, groups of semi-linear transformations of
is taken to be a free module of finite type. Often one means by classical groups other groups closely related to groups of automorphisms of forms (for example, their commutator subgroups or quotients with respect to the centre) or some of their extensions (for example, groups of semi-linear transformations of  preserving
preserving 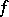 up to a scalar factor and an automorphism of
up to a scalar factor and an automorphism of 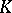 ).
).
Classical groups are closely related to geometry: They can be characterized as groups of those transformations of projective spaces (and also of certain varieties related to Grassmannians, see [2]) that preserve the natural incidence relations. For example, according to the fundamental theorem of projective geometry, the group of all transformations of  -dimensional projective space
-dimensional projective space 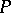 over a skew-field
over a skew-field 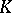 that preserve collinearity coincides for
that preserve collinearity coincides for 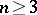 with the classical group of all projective collineations of
with the classical group of all projective collineations of 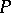 . For this reason, the study of the structure of a classical group has a geometrical meaning; it is equivalent to the study of the symmetries (automorphisms) of the corresponding geometry.
. For this reason, the study of the structure of a classical group has a geometrical meaning; it is equivalent to the study of the symmetries (automorphisms) of the corresponding geometry.
The theory of classical groups has been developed most profoundly for the case when 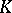 is a skew-field and
is a skew-field and 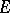 is a vector space of finite dimension
is a vector space of finite dimension  over
over 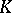 . From now on, these conditions will be assumed to hold. Then the groups of the following series (to be described below) are usually called classical:
. From now on, these conditions will be assumed to hold. Then the groups of the following series (to be described below) are usually called classical: 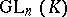 ,
, 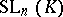 ,
, 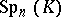 ,
, 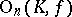 ,
, 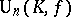 .
.
1) Let 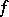 be the null form. Then the group of all automorphisms of
be the null form. Then the group of all automorphisms of 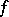 is the same as the group of all automorphisms of
is the same as the group of all automorphisms of 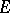 (that is, bijective linear mappings from
(that is, bijective linear mappings from  into
into 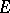 ); it is denoted by
); it is denoted by 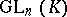 and is called the general linear group in
and is called the general linear group in  variables over the skew-field
variables over the skew-field 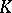 , sometimes the full linear group. The subgroup of
, sometimes the full linear group. The subgroup of  generated by all transvections (cf. Transvection) is denoted by
generated by all transvections (cf. Transvection) is denoted by 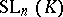 and is called the special linear group (or unimodular group) in
and is called the special linear group (or unimodular group) in  variables over the skew-field
variables over the skew-field 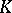 . It is the same as the set of automorphisms with determinant
. It is the same as the set of automorphisms with determinant 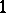 .
.
2) Let 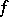 be a non-degenerate sesquilinear form (with respect to an involution
be a non-degenerate sesquilinear form (with respect to an involution 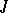 of
of 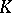 ) for which the orthogonality relation is symmetric, that is
) for which the orthogonality relation is symmetric, that is
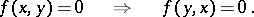 |
Such a form is called reflexive. The group 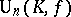 of all automorphisms of
of all automorphisms of 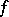 is called the unitary group in
is called the unitary group in  variables over the skew-field
variables over the skew-field 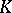 with respect to the form
with respect to the form 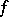 . There are only two possibilities: Either
. There are only two possibilities: Either 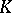 is a field,
is a field, 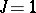 and
and 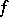 is a skew-symmetric bilinear form, or by multiplying
is a skew-symmetric bilinear form, or by multiplying 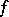 by a suitable scalar and altering
by a suitable scalar and altering 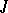 , one can arrange for
, one can arrange for 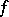 to be a Hermitian or skew-Hermitian form. For a skew-symmetric form
to be a Hermitian or skew-Hermitian form. For a skew-symmetric form 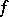 ,
, 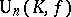 is called the symplectic group in
is called the symplectic group in  variables over the skew-field
variables over the skew-field 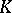 (if
(if 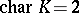 one must suppose that
one must suppose that 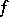 is an alternating form); it is denoted by
is an alternating form); it is denoted by 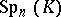 . This notation does not include
. This notation does not include 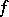 because all non-degenerate alternating forms on
because all non-degenerate alternating forms on 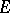 are equivalent and define isomorphic symplectic groups. In this case
are equivalent and define isomorphic symplectic groups. In this case  is even. For Hermitian and skew-Hermitian forms, there is the special case that
is even. For Hermitian and skew-Hermitian forms, there is the special case that 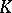 is a field of characteristic different from 2,
is a field of characteristic different from 2, 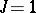 and
and 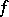 is a symmetric bilinear form. Then
is a symmetric bilinear form. Then 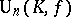 is called the orthogonal group in
is called the orthogonal group in  variables over the field
variables over the field 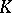 with respect to the form
with respect to the form 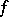 ; it is denoted by
; it is denoted by 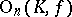 . Orthogonal groups can also be defined for fields of characteristic 2 (see [2]). Often the term "unitary group" is used in a narrower sense for groups
. Orthogonal groups can also be defined for fields of characteristic 2 (see [2]). Often the term "unitary group" is used in a narrower sense for groups 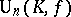 that are neither orthogonal nor symplectic, that is, groups corresponding to non-trivial involutions
that are neither orthogonal nor symplectic, that is, groups corresponding to non-trivial involutions 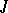 .
.
Associated with each of the fundamental series of classical groups are their projective images 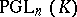 ,
, 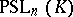 ,
, 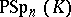 ,
, 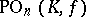 ,
, 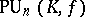 ; these are the quotient groups of them by the intersections with the centre
; these are the quotient groups of them by the intersections with the centre 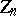 of
of 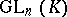 . The group
. The group
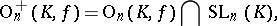 |
the commutator subgroup 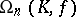 of
of 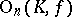 , the group
, the group
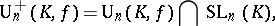 |
and their projective images are also associated with the series of orthogonal and unitary classical groups, respectively.
The classical approach to the theory of classical groups aims at the elucidation of their algebraic structure. This reduces to the description of a normal series of subgroups and their successive quotient groups (in particular a description of normal subgroups and simple composition factors), the description of the automorphisms and isomorphisms of the classical groups (and, more generally, of the homomorphisms), the description of the various types of generating sets and their relations, etc. The main results on the structure of groups of type 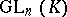 and
and 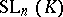 are the following. The commutator subgroup of
are the following. The commutator subgroup of 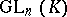 ,
, 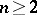 , is
, is 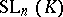 , except in the case
, except in the case 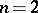 ,
, 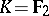 (where
(where 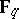 is the field of
is the field of 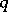 elements). The centre
elements). The centre 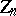 of
of 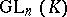 consists of all homotheties
consists of all homotheties 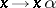 , where
, where 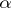 is an element of the centre of
is an element of the centre of 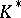 . There is a normal series of subgroups
. There is a normal series of subgroups
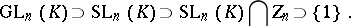 |
The group 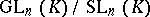 is isomorphic to
is isomorphic to 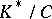 , where
, where 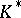 is the multiplicative group of the skew-field
is the multiplicative group of the skew-field  and
and 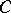 is its commutator subgroup. The group
is its commutator subgroup. The group 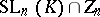 is the centre of
is the centre of 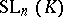 and the quotient group
and the quotient group
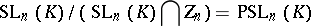 |
is simple in all cases except when 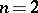 ,
, 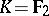 or
or 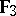 . For further details see General linear group; Special linear group; Symplectic group; Orthogonal group; Unitary group. The structure of a classical group depends essentially on its type, the skew-field
. For further details see General linear group; Special linear group; Symplectic group; Orthogonal group; Unitary group. The structure of a classical group depends essentially on its type, the skew-field 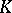 , the properties of the form
, the properties of the form 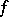 , and
, and  . For some types of classical groups a very detailed description is available. For others there are still open questions. (These involve mainly groups of type
. For some types of classical groups a very detailed description is available. For others there are still open questions. (These involve mainly groups of type 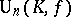 where
where 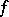 is an anisotropic form.) Typical for the structure theory of classical groups are assertions that hold for almost-all
is an anisotropic form.) Typical for the structure theory of classical groups are assertions that hold for almost-all 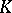 ,
, 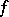 and
and  , and the investigation of the various exceptional cases when these assertions are false. (Such exceptions arise for instance for small values of
, and the investigation of the various exceptional cases when these assertions are false. (Such exceptions arise for instance for small values of  , for finite fields
, for finite fields 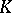 of small order or for special values of the index of the form
of small order or for special values of the index of the form 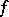 .)
.)
The question of isomorphisms of classical groups occupies a special position. First there are the standard isomorphisms. These are isomorphisms between 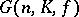 and
and  the definition of which does not depend on special properties of
the definition of which does not depend on special properties of 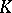 (except, perhaps, its commutativity). All other isomorphisms are called non-standard. For example, there is a (standard) isomorphism from
(except, perhaps, its commutativity). All other isomorphisms are called non-standard. For example, there is a (standard) isomorphism from 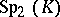 onto
onto 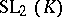 , where
, where 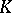 is any field, or from
is any field, or from 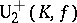 onto
onto 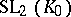 , where
, where 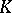 is any field,
is any field, 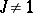 ,
, 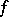 is a form of index 1, and
is a form of index 1, and 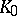 is the field of invariants of
is the field of invariants of 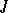 . For a detailed description of the known standard isomorphisms, see [2], [3]. Examples of non-standard isomorphisms are:
. For a detailed description of the known standard isomorphisms, see [2], [3]. Examples of non-standard isomorphisms are:
 |
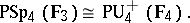 |
It is also known that the groups 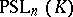 and
and 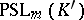 ,
, 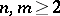 , can be isomorphic only when
, can be isomorphic only when 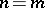 , apart from the case
, apart from the case
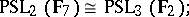 |
when 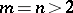 , isomorphism is possible only if
, isomorphism is possible only if 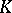 and
and 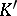 are isomorphic or anti-isomorphic; this is also the case when
are isomorphic or anti-isomorphic; this is also the case when 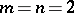 if
if 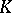 and
and 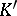 are fields, apart from the case
are fields, apart from the case
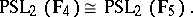 |
The groups 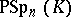 and
and 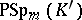 can be isomorphic only if
can be isomorphic only if 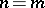 and
and 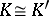 , apart from the case
, apart from the case 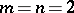 ,
, 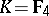 ,
, 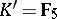 . There are no other isomorphisms among the groups
. There are no other isomorphisms among the groups 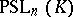 ,
, 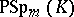 ,
, 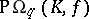 (where
(where 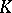 is a finite field) apart from the ones indicated above.
is a finite field) apart from the ones indicated above.
The results listed above on the structure of classical groups and their isomorphisms are obtained by methods of linear algebra and projective geometry. The basis for this consists in the study of special elements in the classical groups and the geometric properties of them, principally the study of transvections, involutions and planar rotations. Subsequently, methods of the theory of Lie groups and algebraic geometry were introduced into the theory of classical groups, whereupon the theory of classical groups became much related with the general theory of semi-simple linear algebraic groups in which classical groups appear as forms (cf. Form of an algebraic group): Every form of a simple linear algebraic group over a field 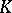 of classical type (that is, of type
of classical type (that is, of type 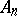 ,
, 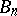 ,
, 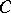 , or
, or 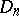 ) gives rise to a classical group, the group of its
) gives rise to a classical group, the group of its 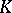 -rational points (an exception being a form of
-rational points (an exception being a form of 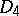 connected with an outer automorphism of order three). In the case when
connected with an outer automorphism of order three). In the case when 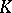 is
is 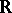 or
or 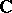 , a classical group is naturally endowed with a Lie group structure, and for
, a classical group is naturally endowed with a Lie group structure, and for 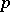 -adic fields with a
-adic fields with a 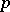 -adic analytic group structure. This makes it possible to use topological methods in the study of such classical groups, and conversely, to obtain information on the topological structure of the underlying variety of a classical group (for example, on its finite cellular decompositions) from the knowledge of its algebraic structure.
-adic analytic group structure. This makes it possible to use topological methods in the study of such classical groups, and conversely, to obtain information on the topological structure of the underlying variety of a classical group (for example, on its finite cellular decompositions) from the knowledge of its algebraic structure.
In the more general situation when 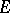 is a module over a ring
is a module over a ring 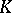 the results on classical groups are not so exhaustive (see [3]). Here the theory of classical groups links up with algebraic
the results on classical groups are not so exhaustive (see [3]). Here the theory of classical groups links up with algebraic 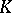 -theory.
-theory.
References
| [1] | E. Artin, "Geometric algebra" , Interscience (1957) |
| [2] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [3] | A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) |
| [4] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
Comments
Instead of [3] one may consult [a1], [a2], [a3].
References
| [a1] | A. Borel, J. Tits, "Homomorphisms "abstraits" de groupes algébriques simples" Ann. of Math. (2) , 97 (1973) pp. 499–571 |
| [a2] | O.T. O'Meara, "A survey of the isomorphism theory of the classical groups" , Ring theory and algebra , 3 , M. Dekker (1980) pp. 225–242 |
| [a3] | A. Weil, "Algebras with involutions and the classical groups" J. Ind. Math. Soc. , 24 (1960) pp. 589–623 |
Classical group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Classical_group&oldid=12596