L-algebra
lattice-ordered algebra
An algebraic system 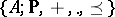 over a totally ordered field
over a totally ordered field 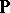 such that
such that 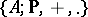 is an associative algebra over
is an associative algebra over 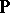 (cf. Associative rings and algebras),
(cf. Associative rings and algebras), 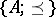 is a lattice respect with the partial order
is a lattice respect with the partial order 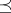 and the following axioms hold:
and the following axioms hold:
1) for all 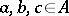 ,
,
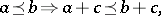 |
2) for all 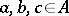 ,
,
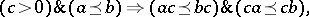 |
3) for all  and
and  ,
,
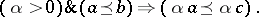 |
An 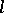 -algebra
-algebra 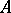 is called a strict
is called a strict 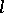 -algebra if for
-algebra if for  and
and 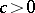 one has
one has 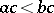 ,
, 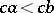 . It is useful to describe an
. It is useful to describe an 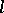 -algebra
-algebra 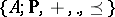 as an algebraic system of signature
as an algebraic system of signature  , where
, where 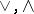 are the join and meet operations in the lattice
are the join and meet operations in the lattice 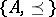 .
.
The most important examples of 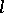 -algebras are: the
-algebras are: the 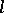 -algebra
-algebra 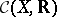 of all continuous real-valued functions on a topological space
of all continuous real-valued functions on a topological space  with respect to the natural operations and equipped with the order
with respect to the natural operations and equipped with the order 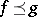 , for
, for 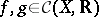 , if and only if
, if and only if 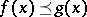 for all
for all 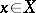 ; and the
; and the 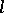 -algebra
-algebra 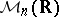 of all
of all 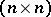 -matrices over
-matrices over  with order
with order 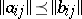 if and only if
if and only if 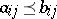 for all
for all 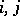 .
.
A homomorphism 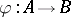 of
of 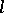 -algebras
-algebras 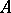 and
and 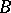 is an
is an 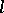 -homomorphism if
-homomorphism if  is a homomorphism of the algebras
is a homomorphism of the algebras 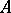 and
and 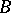 and a homomorphism of the lattices
and a homomorphism of the lattices 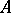 and
and 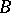 . The kernel of an
. The kernel of an 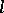 -homomorphism of
-homomorphism of 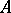 is an
is an  -ideal, i.e., an ideal of
-ideal, i.e., an ideal of 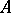 that is also a convex sublattice of
that is also a convex sublattice of 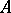 .
.
If 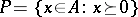 , then
, then 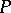 is called the positive cone of the
is called the positive cone of the 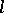 -algebra
-algebra 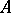 . For the positive cone
. For the positive cone 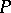 of an
of an 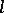 -algebra
-algebra 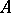 the following properties hold:
the following properties hold:
1) 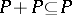 ;
;
2) 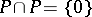 ;
;
3) 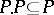 ;
;
4) 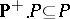 ;
;
5) 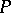 is a lattice respect with the induced order. Here,
is a lattice respect with the induced order. Here, 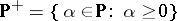 . If, in an algebra
. If, in an algebra 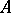 over
over 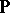 , one can find a subset
, one can find a subset 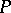 with the properties 1)–5), then
with the properties 1)–5), then 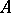 can be given the structure of an
can be given the structure of an 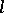 -algebra with positive cone
-algebra with positive cone 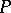 by setting:
by setting: 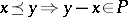 for
for 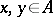 . It is correct to identify the order of an
. It is correct to identify the order of an 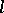 -algebra with its positive cone, and so an
-algebra with its positive cone, and so an 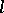 -algebra
-algebra 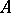 is often denoted by
is often denoted by 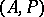 .
.
An 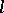 -algebra
-algebra 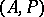 is strict if and only if
is strict if and only if 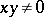 for all
for all  .
.
An 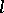 -algebra
-algebra 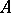 is totally-ordered (an
is totally-ordered (an  -algebra) if its order is total (cf. also Totally ordered set). An
-algebra) if its order is total (cf. also Totally ordered set). An 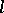 -algebra is called an
-algebra is called an 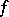 -algebra if it is an
-algebra if it is an  -subalgebra of the Cartesian product of
-subalgebra of the Cartesian product of  -algebras. An
-algebras. An 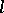 -algebra
-algebra 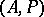 is an
is an 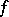 -algebra if and only if there exists a set
-algebra if and only if there exists a set 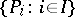 of total orders on
of total orders on 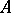 such that
such that 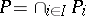 .
.  - and
- and 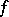 -algebras have been well investigated. Every Archimedean
-algebras have been well investigated. Every Archimedean 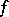 -algebra over
-algebra over 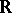 is commutative. The set
is commutative. The set 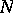 of nilpotent elements in an
of nilpotent elements in an  -algebra
-algebra 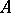 is a convex ideal of
is a convex ideal of 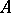 and the quotient algebra
and the quotient algebra 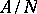 has no zero divisors. There exists a full description of the finite-dimensional
has no zero divisors. There exists a full description of the finite-dimensional  -algebras. An
-algebras. An 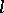 -algebra
-algebra 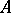 is an
is an 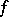 -algebra if and only if for all
-algebra if and only if for all 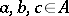 ,
,
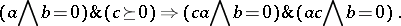 |
The structure of the convex 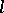 -subalgebras and prime ideals has been investigated.
-subalgebras and prime ideals has been investigated.
The theory of 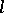 -algebras is used in the study of order-preserving linear transformations and orthomorphisms of ordered vector spaces (i.e., linear transformations preserving the orthogonality properties).
-algebras is used in the study of order-preserving linear transformations and orthomorphisms of ordered vector spaces (i.e., linear transformations preserving the orthogonality properties).
References
| [a1] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
| [a2] | A. Bigard, K. Keimel, S. Wolfenstein, "Groupes et anneaux rétiqulés" , Springer (1977) |
L-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L-algebra&oldid=12581