Salem number
An algebraic integer  (cf. Algebraic number) such that all other Galois conjugates of
(cf. Algebraic number) such that all other Galois conjugates of  lie inside the closed unit disc
lie inside the closed unit disc  , with at least one lying on the boundary (cf. also Galois theory). One should compare this definition with that of a Pisot number. The set of Salem numbers is traditionally denoted by
, with at least one lying on the boundary (cf. also Galois theory). One should compare this definition with that of a Pisot number. The set of Salem numbers is traditionally denoted by  . If
. If  is a Salem number, then it is reciprocal in the sense that its minimal polynomial
is a Salem number, then it is reciprocal in the sense that its minimal polynomial  satisfies
satisfies  , where
, where 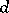 is the degree of
is the degree of  , so
, so 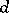 is even and
is even and  . Two of the conjugates of
. Two of the conjugates of  are real, namely
are real, namely  and
and  , and the rest lie on the unit circle. The field
, and the rest lie on the unit circle. The field  is thus a quadratic extension (cf. Extension of a field) of the totally real field
is thus a quadratic extension (cf. Extension of a field) of the totally real field  , so not all number fields contain Salem numbers, in contrast to the situation for Pisot numbers [a1].
, so not all number fields contain Salem numbers, in contrast to the situation for Pisot numbers [a1].
If  is a Pisot or Salem number, then, given
is a Pisot or Salem number, then, given  , there is a positive number
, there is a positive number 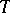 such that every interval of real numbers contains a
such that every interval of real numbers contains a  such that
such that  for all
for all 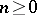 . Here
. Here  denotes the distance from
denotes the distance from  to the nearest integer. This property characterizes the Pisot and Salem numbers among the real numbers [a3]. This property leads to applications in harmonic analysis, dynamical systems theory (cf. also Dynamical system) and the theory of quasi-crystals, cf. also Pisot number.
to the nearest integer. This property characterizes the Pisot and Salem numbers among the real numbers [a3]. This property leads to applications in harmonic analysis, dynamical systems theory (cf. also Dynamical system) and the theory of quasi-crystals, cf. also Pisot number.
Each Pisot number  is the limit from both sides of a sequence of Salem numbers. The proof of this gives an explicit construction of infinitely many Salem numbers from each Pisot number. In fact, every Salem number arises infinitely many times in this construction [a2].
is the limit from both sides of a sequence of Salem numbers. The proof of this gives an explicit construction of infinitely many Salem numbers from each Pisot number. In fact, every Salem number arises infinitely many times in this construction [a2].
It is an open question whether the Salem numbers are dense in  , but it has been conjectured that if
, but it has been conjectured that if 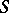 is the set of Pisot numbers, then
is the set of Pisot numbers, then 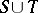 is closed. This would imply that
is closed. This would imply that  is nowhere dense. All the Salem numbers smaller than
is nowhere dense. All the Salem numbers smaller than  and of degree at most
and of degree at most  are known, see [a4]. The smallest known Salem number is the number
are known, see [a4]. The smallest known Salem number is the number 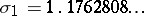 of degree
of degree  known as Lehmer's number. The minimum polynomial of
known as Lehmer's number. The minimum polynomial of  is Lehmer's polynomial:
is Lehmer's polynomial:  . This is also the smallest known value
. This is also the smallest known value  of the Mahler measure.
of the Mahler measure.
References
| [a1] | M.J. Bertin, A. Decomps–Guilloux, M. Grandet–Hugot, M. Pathiaux–Delefosse, J.P. Schreiber, "Pisot and Salem Numbers" , Birkhäuser (1992) |
| [a2] | D.W. Boyd, "Small Salem numbers" Duke Math. J. , 44 (1977) pp. 315–328 |
| [a3] | Y. Meyer, "Algebraic numbers and harmonic analysis" , North-Holland (1972) |
| [a4] | M.J. Mossinghoff, "Small Salem numbers" , web page: http://www.math.ucla.edu/~mjm/lc/lists/SalemList.html (1998) |
Salem number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Salem_number&oldid=12578