Delaunay triangulation
From Encyclopedia of Mathematics
Delone triangulation
A very important geometric structure in computational geometry, named after B.N. Delaunay.
Let 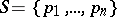 be a generic set of
be a generic set of  points in
points in 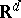 . The straight-line dual of the Voronoi diagram generated by
. The straight-line dual of the Voronoi diagram generated by 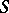 is a triangulation of
is a triangulation of 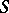 , called the Delaunay triangulation and usually denoted by
, called the Delaunay triangulation and usually denoted by 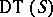 . The Delaunay triangulation of
. The Delaunay triangulation of 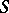 is triangulation of the convex hull of
is triangulation of the convex hull of 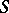 in
in 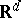 and the set of vertices of
and the set of vertices of 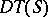 is
is 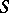 .
.
One of the equivalent definitions for 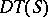 is as follows:
is as follows: 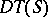 is a triangulation of
is a triangulation of 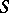 satisfying the "empty sphere propertyempty sphere property" , i.e. no
satisfying the "empty sphere propertyempty sphere property" , i.e. no  -simplex of the triangulation of its circumsphere has a point of
-simplex of the triangulation of its circumsphere has a point of 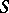 in its interior.
in its interior.
References
| [a1] | F.P. Preparata, M.I. Shamos, "Computational geometry: an introduction" , Springer (1985) |
| [a2] | H. Edelsbrunner, "Algorithms in combinatorial geometry" , Springer (1987) |
| [a3] | A. Okabe, B. Boots, K. Sugihara, "Spatial tessellations: concepts and applications of Voronoi diagrams" , Wiley (1992) |
How to Cite This Entry:
Delaunay triangulation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Delaunay_triangulation&oldid=12570
Delaunay triangulation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Delaunay_triangulation&oldid=12570
This article was adapted from an original article by O.R. Musin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article