Focus

A type of arrangement of the trajectories of an autonomous system of first-order ordinary differential equations

(*)

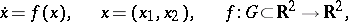, where is the domain of uniqueness, in a neighbourhood of a singular point (cf. Equilibrium position). This type is characterized as follows. There is a neighbourhood of such that for all trajectories of the system starting in , the negative semi-trajectories are escaping (in the course of time they leave any compact set ) and the positive semi-trajectories, without leaving , tend to 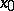, winding round it like a logarithmic spiral, or conversely. The point 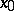itself is also called a focus. The nature of the approach of the trajectories of the system to can be described more precisely if one introduces polar coordinates on the -plane with pole at . Then for any semi-trajectory , , 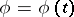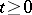(), that tends to , the polar angle of the variable point 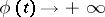(a left focus) or (a right focus) as .

A focus is either asymptotically Lyapunov stable or completely unstable (asymptotically stable as ). Its Poincaré index is 1. The figure depicts a right unstable focus at .

Figure: f040700a

For a system (*) of class () a singular point is a focus in case the matrix has complex conjugate eigen values with non-zero real part, but it may also be a focus in case this matrix has purely imaginary or multiple real eigen values (see also Centre; Centre and focus problem).

For references see Singular point of a differential equation.

References

[a1]	P. Hartman, "Ordinary differential equations" , Birkhäuser (1982)