Bernstein-Rogosinski summation method
One of the methods for summing Fourier series; denoted by 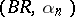 . A trigonometric series
. A trigonometric series
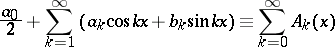 | (*) |
is summable by the Bernstein–Rogosinski method at a point 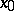 to the value
to the value 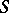 if the following condition is satisfied:
if the following condition is satisfied:
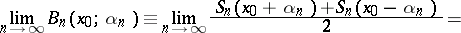 |
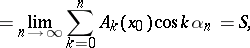 |
where 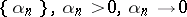 , is a sequence of numbers, and where the
, is a sequence of numbers, and where the 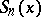 are the partial sums of the series (*).
are the partial sums of the series (*).
W. Rogosinski [1] first (1924) considered the case 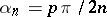 , where
, where 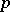 is an odd number, and then (1925) the general case. S.N. Bernstein [S.N. Bernshtein] [2] considered (1930) the case
is an odd number, and then (1925) the general case. S.N. Bernstein [S.N. Bernshtein] [2] considered (1930) the case 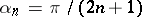 . The
. The 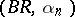 -method sums the Fourier series of a function
-method sums the Fourier series of a function 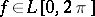 in the cases
in the cases 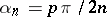 and
and 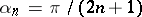 at the points of continuity of the function to its value and is one of the regular summation methods.
at the points of continuity of the function to its value and is one of the regular summation methods.
The Bernstein–Rogosinski sums 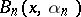 are employed as an approximation procedure. In both cases described above they realize an approximation of the same order as the best approximation for functions of the classes
are employed as an approximation procedure. In both cases described above they realize an approximation of the same order as the best approximation for functions of the classes 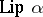 and
and 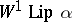 .
.
References
| [1] | W.W. Rogosinski, "Ueber die Abschnitte trigonometischer Reihen" Math. Ann. , 95 (1925) pp. 110–134 |
| [2] | S.N. Bernshtein, , Collected works , 1 , Moscow (1952) pp. 37 |
| [3] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
Comments
References
| [a1] | W. Beekmann, K. Zeller, "Theorie der Limitierungsverfahren" , Springer (1970) |
Bernstein-Rogosinski summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein-Rogosinski_summation_method&oldid=12552