Asymptotically-unbiased estimator
A concept indicating that the estimator is unbiased in the limit (cf. Unbiased estimator). Let 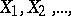 be a sequence of random variables on a probability space
be a sequence of random variables on a probability space 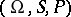 , where
, where 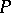 is one of the probability measures in a family
is one of the probability measures in a family 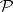 . Let a function
. Let a function 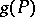 be given on the family
be given on the family 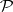 , and let there be a sequence of
, and let there be a sequence of 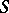 -measurable functions
-measurable functions 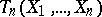 ,
, 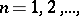 the mathematical expectations of which,
the mathematical expectations of which, 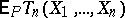 , are given. Then, if, as
, are given. Then, if, as 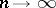 ,
,
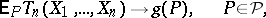 |
one says that 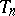 is a function which is asymptotically unbiased for the function
is a function which is asymptotically unbiased for the function 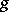 . If one calls
. If one calls  "observations" and
"observations" and 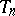 "estimators" , one obtains the definition of an asymptotically-unbiased estimator. In the simplest case of unlimited repeated sampling from a population, the distribution of which depends on a one-dimensional parameter
"estimators" , one obtains the definition of an asymptotically-unbiased estimator. In the simplest case of unlimited repeated sampling from a population, the distribution of which depends on a one-dimensional parameter 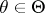 , an asymptotically-unbiased estimator
, an asymptotically-unbiased estimator 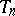 for
for  , constructed with respect to the sample size
, constructed with respect to the sample size  , satisfies the condition
, satisfies the condition
 |
for any 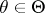 , as
, as  .
.
Asymptotically-unbiased estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotically-unbiased_estimator&oldid=12532