Mean curvature
of a surface 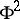 in
in  -dimensional Euclidean space
-dimensional Euclidean space 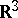
Half of the sum of the principal curvatures (cf. Principal curvature) 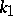 and
and 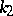 , calculated at a point
, calculated at a point 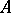 of this surface:
of this surface:
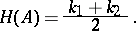 |
For a hypersurface 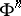 in the Euclidean space
in the Euclidean space 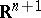 , this formula is generalized in the following way:
, this formula is generalized in the following way:
 |
where 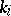 ,
, 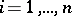 , are the principal curvatures of the hypersurface, calculated at a point
, are the principal curvatures of the hypersurface, calculated at a point 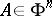 .
.
The mean curvature of a surface in 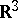 can be expressed by means of the coefficients of the first and second fundamental forms of this surface:
can be expressed by means of the coefficients of the first and second fundamental forms of this surface:
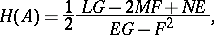 |
where 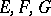 are the coefficients of the first fundamental form, and
are the coefficients of the first fundamental form, and 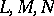 are the coefficients of the second fundamental form, calculated at a point
are the coefficients of the second fundamental form, calculated at a point 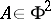 . In the particular case where the surface is defined by an equation
. In the particular case where the surface is defined by an equation 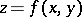 , the mean curvature is calculated using the formula:
, the mean curvature is calculated using the formula:
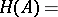 |
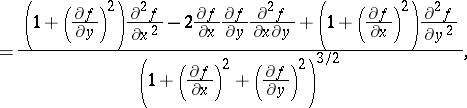 |
which is generalized for a hypersurface 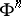 in
in 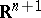 , defined by the equation
, defined by the equation 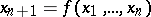 , as follows:
, as follows:
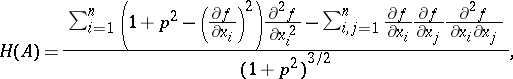 |
where
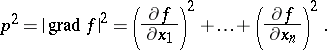 |
Comments
For an 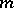 -dimensional submanifold
-dimensional submanifold 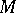 of an
of an  -dimensional Euclidean space of codimension
-dimensional Euclidean space of codimension 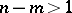 , the mean curvature generalizes to the notion of the mean curvature normal
, the mean curvature generalizes to the notion of the mean curvature normal
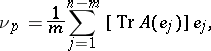 |
where 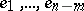 is an orthonormal frame of the normal space (cf. Normal space (to a surface)) of
is an orthonormal frame of the normal space (cf. Normal space (to a surface)) of 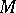 at
at 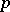 and
and  (
(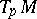 denotes the tangent space to
denotes the tangent space to  at
at 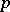 ) is the shape operator of
) is the shape operator of 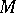 at
at 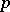 in the direction
in the direction 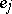 , which is related to the second fundamental tensor
, which is related to the second fundamental tensor 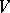 of
of 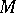 at
at 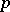 by
by 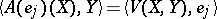 .
.
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) |
| [a3] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
| [a4] | B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973) |
Mean curvature. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mean_curvature&oldid=12526