Regression
Dependence of the mean value of some random variable on another variable or on several variables. If, for example, for every value 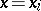 one observes
one observes 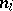 values
values 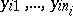 of a random variable
of a random variable 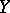 , then the dependence of the arithmetic mean
, then the dependence of the arithmetic mean
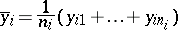 |
of these values on 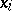 is a regression in the statistical meaning of the term. If
is a regression in the statistical meaning of the term. If 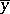 varies systematically with
varies systematically with  , one assumes, on the basis of an observed phenomenon, that there is a probabilistic dependence: For every fixed value
, one assumes, on the basis of an observed phenomenon, that there is a probabilistic dependence: For every fixed value  the random variable
the random variable 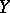 has a definite probability distribution whose mathematical expectation is a function of
has a definite probability distribution whose mathematical expectation is a function of  :
:
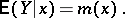 |
The relation 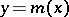 , where
, where  acts as an "independent" variable, is called a regression (or regression function) in the probabilistic sense of the word. The graph of
acts as an "independent" variable, is called a regression (or regression function) in the probabilistic sense of the word. The graph of 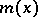 is called the regression line, or regression curve, of
is called the regression line, or regression curve, of 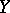 on
on  . The variable
. The variable  is called the regression variable or regressor. The accuracy with which the regression curve of
is called the regression variable or regressor. The accuracy with which the regression curve of 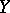 on
on  reflects the average variation of
reflects the average variation of 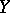 with variation in
with variation in  is measured by the variance of
is measured by the variance of 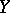 (cf. Dispersion), and is computed for every value as follows:
(cf. Dispersion), and is computed for every value as follows:
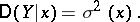 |
Graphically, the dependence of 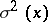 on
on  is expressed by the scedastic curve. If
is expressed by the scedastic curve. If 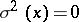 for all values of
for all values of  , then with probability 1 the variables are connected by a perfect functional dependence. If
, then with probability 1 the variables are connected by a perfect functional dependence. If 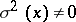 at any value of
at any value of  and
and 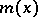 does not depend on
does not depend on  , then regression of
, then regression of 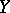 with respect to
with respect to  is absent.
is absent.
In probability theory, the problem of regression is solved in case the values of the regression variable  correspond to the values of a certain random variable
correspond to the values of a certain random variable 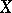 , and it is assumed that one knows the joint probability distribution of the variables
, and it is assumed that one knows the joint probability distribution of the variables 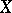 and
and 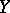 (here, the expectation
(here, the expectation 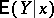 and the variance
and the variance 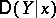 will be the conditional expectation and conditional variance of
will be the conditional expectation and conditional variance of 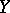 , respectively, for a fixed value
, respectively, for a fixed value 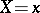 ). In this case, two regressions are defined:
). In this case, two regressions are defined: 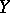 with respect to
with respect to  and
and 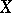 with respect to
with respect to 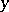 , and the concept of regression can also be used to introduce certain measures of the interrelation between
, and the concept of regression can also be used to introduce certain measures of the interrelation between 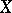 and
and 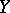 , defined as characteristics of the degree of concentration of the distribution around the regression curves (see Correlation (in statistics)).
, defined as characteristics of the degree of concentration of the distribution around the regression curves (see Correlation (in statistics)).
Regression functions possess the property that among all real-valued functions 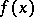 the minimum expectation
the minimum expectation 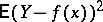 is attained when
is attained when 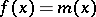 , that is, the regression of
, that is, the regression of 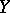 with respect to
with respect to  gives the best (in the above sense) representation of the variable
gives the best (in the above sense) representation of the variable 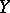 . The most important case is when the regression of
. The most important case is when the regression of 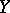 with respect to
with respect to  is linear, that is,
is linear, that is,
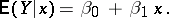 |
The coefficients 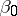 and
and 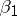 are called regression coefficients, and are easily calculated:
are called regression coefficients, and are easily calculated:
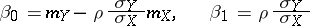 |
(where 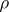 is the correlation coefficient of
is the correlation coefficient of 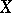 and
and 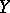 ,
, 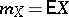 ,
, 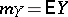 ,
, 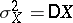 , and
, and 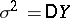 ), and the regression curve of
), and the regression curve of 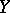 with respect to
with respect to  has the form
has the form
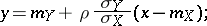 |
the regression curve of 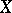 with respect to
with respect to 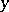 is found in a similar way. The linear regression is exact in the case when the two-dimensional distribution of the variables
is found in a similar way. The linear regression is exact in the case when the two-dimensional distribution of the variables  and
and 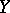 is normal.
is normal.
Under the conditions of statistical applications, when for the exact determination of the regression there are insufficient facts about the form of the joint probability distribution, there arises the problem of the approximate determination of the regression. To solve this problem, one can choose, out of all functions 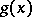 belonging to a given class, that function which gives the best representation of the variable
belonging to a given class, that function which gives the best representation of the variable 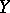 , in the sense that the expectation
, in the sense that the expectation 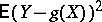 is minimized. This function is called the mean-square (mean-quadratic) regression.
is minimized. This function is called the mean-square (mean-quadratic) regression.
The simplest case is that of linear mean-square regression, when one looks for the best linear approximation to 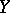 by means of
by means of 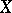 , that is, a linear function
, that is, a linear function 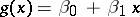 for which the expression
for which the expression 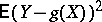 takes the smallest possible value. The given extremal problem has a unique solution:
takes the smallest possible value. The given extremal problem has a unique solution:
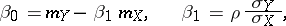 |
that is, the calculation of an approximate regression curve leads to the same result as that obtained in the case of exact linear regression:
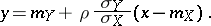 |
The minimal value of 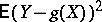 , for calculated values of the parameters, is equal to
, for calculated values of the parameters, is equal to 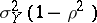 . If a regression
. If a regression 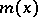 exists, then, for all
exists, then, for all 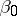 and
and 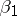 ,
,
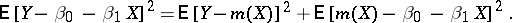 |
This implies that the mean-square regression curve 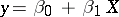 gives the best approximation along the
gives the best approximation along the 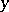 -axis. Therefore, if the curve
-axis. Therefore, if the curve 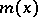 is a straight line, it coincides with the mean-square regression line.
is a straight line, it coincides with the mean-square regression line.
In the general case, when the regression is far from being linear, one can pose the problem of finding a polynomial 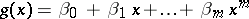 of a certain degree
of a certain degree 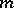 for which
for which 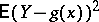 is as small as possible.
is as small as possible.
A solution of this problem corresponds to polynomial mean-square regression (see Parabolic regression). The function 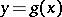 is a polynomial of order
is a polynomial of order 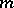 , and gives the best approximation to the true regression curve. A generalization of polynomial regression is the regression function expressed as a linear combination of certain given functions:
, and gives the best approximation to the true regression curve. A generalization of polynomial regression is the regression function expressed as a linear combination of certain given functions:
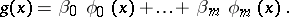 |
The most important case is when 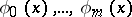 are orthogonal polynomials of corresponding orders constructed from the distribution of
are orthogonal polynomials of corresponding orders constructed from the distribution of 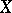 . There are other examples of non-linear (curvilinear) regression, such as trigonometric regression and exponential regression.
. There are other examples of non-linear (curvilinear) regression, such as trigonometric regression and exponential regression.
The concept of regression can be extended in a natural way to the case where, instead of one regression variable, some set of variables is considered. If the random variables 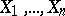 have a joint probability distribution, then one can define a multiple regression, e.g. as the regression of
have a joint probability distribution, then one can define a multiple regression, e.g. as the regression of 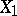 with respect to
with respect to  :
:
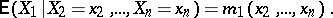 |
The corresponding equation defines the regression surface of 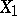 with respect to
with respect to  . The linear regression of
. The linear regression of 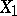 with respect to
with respect to  has the form
has the form
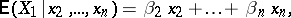 |
where  are the regression coefficients (if
are the regression coefficients (if 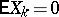 ). The linear mean-square regression of
). The linear mean-square regression of 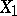 with respect to
with respect to  is defined as the best linear estimator of the variable
is defined as the best linear estimator of the variable 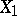 in terms of the variables
in terms of the variables 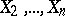 , in the sense that
, in the sense that
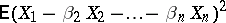 |
is minimized. The corresponding regression plane gives the best approximation to the regression surface 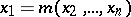 , if the latter exists. If the regression surface is a plane, then it necessarily coincides with the mean-square regression plane (as happens in the case when the joint distribution of all
, if the latter exists. If the regression surface is a plane, then it necessarily coincides with the mean-square regression plane (as happens in the case when the joint distribution of all  variables is normal).
variables is normal).
A simple example of regression of 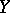 with respect to
with respect to 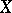 is given by the dependence between
is given by the dependence between 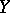 and
and 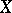 expressed by the relation
expressed by the relation 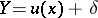 , where
, where 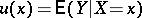 , where
, where 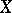 and
and 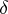 are independent random variables. This representation is useful when designing an experiment for studying a functional relation
are independent random variables. This representation is useful when designing an experiment for studying a functional relation 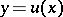 between two non-random variables
between two non-random variables 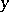 and
and  . The same regression model is used in numerous applications to study the nature of dependence of a random variable
. The same regression model is used in numerous applications to study the nature of dependence of a random variable 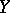 on a non-random variable
on a non-random variable  . In practice, the choice of the function
. In practice, the choice of the function 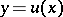 and the estimation of the unknown regression coefficients by experimental data are made using methods of regression analysis.
and the estimation of the unknown regression coefficients by experimental data are made using methods of regression analysis.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
Regression. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regression&oldid=12502