Lie algebras, variety of
over a ring 
A class  of Lie algebras (cf. Lie algebra) over
of Lie algebras (cf. Lie algebra) over  that satisfy a fixed system of identities. The most prevalent varieties of Lie algebras are the following: the variety
that satisfy a fixed system of identities. The most prevalent varieties of Lie algebras are the following: the variety  of Abelian Lie algebras specified by the identity
of Abelian Lie algebras specified by the identity  , the variety
, the variety  of nilpotent Lie algebras of class
of nilpotent Lie algebras of class  (in which any products of length greater than
(in which any products of length greater than  are equal to zero), the variety
are equal to zero), the variety  of solvable Lie algebras of length
of solvable Lie algebras of length 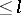 (in which the derived series converges to zero in no more than
(in which the derived series converges to zero in no more than 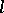 steps). The totality
steps). The totality 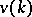 of all varieties of Lie algebras over
of all varieties of Lie algebras over 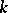 is a groupoid with respect to multiplication:
is a groupoid with respect to multiplication: 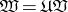 , where
, where 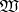 is the class of extensions of algebras from
is the class of extensions of algebras from  by means of ideals from
by means of ideals from  ;
; 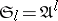 ; the algebras of
; the algebras of 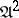 are called metabelian.
are called metabelian.
The central problem in the theory of varieties of Lie algebras is to describe bases of identities of a variety of Lie algebras, in particular whether they are finite or infinite (if 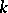 is a Noetherian ring). If
is a Noetherian ring). If 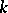 is a field of characteristic
is a field of characteristic 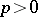 , there are examples of locally finite varieties of Lie algebras lying in
, there are examples of locally finite varieties of Lie algebras lying in  and not having a finite basis of identities. In the case of a field
and not having a finite basis of identities. In the case of a field  of characteristic 0 there are no examples up till now (1989) of infinitely based varieties. The finite basis property is preserved under right multiplication by a nilpotent variety and under union with such a variety. Among the Specht varieties (that is, those in which every variety is finitely based) are the varieties of Lie algebras
of characteristic 0 there are no examples up till now (1989) of infinitely based varieties. The finite basis property is preserved under right multiplication by a nilpotent variety and under union with such a variety. Among the Specht varieties (that is, those in which every variety is finitely based) are the varieties of Lie algebras 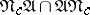 over any Noetherian ring,
over any Noetherian ring, 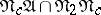 over any field of characteristic
over any field of characteristic  , and
, and  , defined by identities that are true in the Lie algebra
, defined by identities that are true in the Lie algebra  of matrices of order 2 over a field
of matrices of order 2 over a field 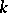 with
with 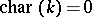 . Over a field
. Over a field 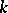 of characteristic 0 there are still no examples of a finite-dimensional Lie algebra
of characteristic 0 there are still no examples of a finite-dimensional Lie algebra 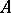 such that
such that 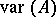 is infinitely based, but there are such examples over an infinite field
is infinitely based, but there are such examples over an infinite field 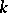 of characteristic
of characteristic 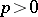 . Over a finite field, or, more generally, over any finite ring
. Over a finite field, or, more generally, over any finite ring  with a unit, the identities of a finite Lie algebra
with a unit, the identities of a finite Lie algebra 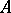 follow from a finite subsystem of them.
follow from a finite subsystem of them.
A variety of Lie algebras 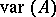 generated by a finite algebra
generated by a finite algebra 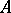 is called a Cross variety and is contained in a Cross variety
is called a Cross variety and is contained in a Cross variety 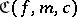 consisting of Lie algebras in which all principal factors have order
consisting of Lie algebras in which all principal factors have order 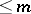 , all nilpotent factors have class
, all nilpotent factors have class  and all inner derivations
and all inner derivations 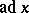 are annihilated by a unitary polynomial
are annihilated by a unitary polynomial 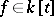 . Just non-Cross varieties (that is, non-Cross varieties all proper subvarieties of which are Cross varieties) have been described in the solvable case, and there are examples of non-solvable just non-Cross varieties. The groupoid
. Just non-Cross varieties (that is, non-Cross varieties all proper subvarieties of which are Cross varieties) have been described in the solvable case, and there are examples of non-solvable just non-Cross varieties. The groupoid  over an infinite field is a free semi-group with 0 and 1, and over a finite field
over an infinite field is a free semi-group with 0 and 1, and over a finite field 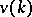 cannot be associative. The lattice
cannot be associative. The lattice 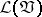 of subvarieties of a variety of Lie algebras
of subvarieties of a variety of Lie algebras  over a field
over a field  is modular, but not distributive in general (cf. Modular lattice; Distributive lattice). The lattice
is modular, but not distributive in general (cf. Modular lattice; Distributive lattice). The lattice 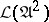 is distributive only in the case of an infinite field. Bases of identities of specific Lie algebras have been found only in a few non-trivial cases: for
is distributive only in the case of an infinite field. Bases of identities of specific Lie algebras have been found only in a few non-trivial cases: for 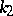 (
(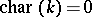 or
or 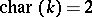 ), and also for some metabelian Lie algebras. Important results have been obtained concerning Lie algebras with the identity
), and also for some metabelian Lie algebras. Important results have been obtained concerning Lie algebras with the identity  (see Lie algebra, nil).
(see Lie algebra, nil).
References
| [1] | V.A. Artamonov, "Lattices of varieties of linear algebras" Russian Math. Surveys , 33 : 2 (1978) pp. 155–193 Uspekhi Mat. Nauk , 33 : 2 (1978) pp. 135–167 |
| [2] | R.K. Amayo, I. Stewart, "Infinite-dimensional Lie algebras" , Noordhoff (1974) |
| [3] | Yu.A. Bakhturin, "Lectures on Lie algebras" , Akademie Verlag (1978) |
| [4] | Yu.A. Bakhturin, "Identical relations in Lie algebras" , VNU , Utrecht (1987) |
Lie algebras, variety of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebras,_variety_of&oldid=12482