Euler numbers

The coefficients 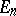in the expansion

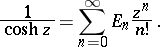The recurrence formula for the Euler numbers (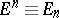 in symbolic notation) has the form

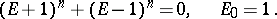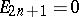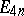Thus, , the are positive and the 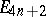are negative integers for all 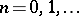; , , 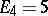, , 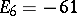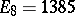and . The Euler numbers are connected with the Bernoulli numbers 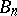by the formulas

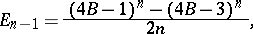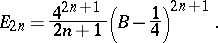The Euler numbers are used in the summation of series. For example,

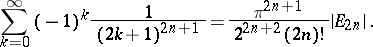Sometimes the 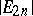are called the Euler numbers.

These numbers were introduced by L. Euler (1755).

References

[1]	L. Euler, "Institutiones calculi differentialis" G. Kowalewski (ed.) , Opera Omnia Ser. 1; opera mat. , 10 , Teubner (1980)
[2]	I.S. Gradshtein, I.M. Ryzhik, "Table of integrals, series and products" , Acad. Press (1980) (Translated from Russian)

Comments

The symbolic formula 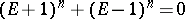should be interpreted as follows: first expand the left-hand side as a sum of the powers 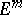, then replace 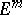with 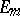. Similarly for the formula connecting the Bernoulli and Euler numbers. The Euler numbers 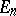are obtained from the Euler polynomials 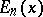by .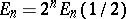

References

[a1]	A. Segun, M. Abramowitz, "Handbook of mathematical functions" , Appl. Math. Ser. , 55 , Nat. Bur. Standards (1970)