Artin root numbers
A global Artin root number is a complex number 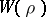 of modulus
of modulus 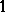 appearing in the functional equation of an Artin
appearing in the functional equation of an Artin 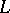 -series (cf. also
-series (cf. also 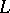 -function)
-function)
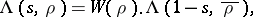 | (a1) |
in which 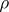 is a representation
is a representation
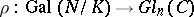 |
of the Galois group of a finite Galois extension 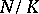 of global fields (cf. also Representation theory; Galois theory; Extension of a field),
of global fields (cf. also Representation theory; Galois theory; Extension of a field), 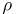 denotes the complex-conjugate representation, and
denotes the complex-conjugate representation, and 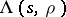 is the (extended) Artin
is the (extended) Artin 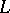 -series with gamma factors at the Archimedean places of
-series with gamma factors at the Archimedean places of 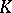 (details can be found in [a6]).
(details can be found in [a6]).
Work of R. Langlands (unpublished) and P. Deligne [a2] shows that the global Artin root number can be written canonically as a product
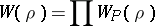 |
of other complex numbers of modulus 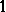 , called local Artin root numbers (Deligne calls them simply "local constants" ). Given
, called local Artin root numbers (Deligne calls them simply "local constants" ). Given 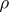 , there is one local root number
, there is one local root number 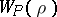 for each non-trivial place
for each non-trivial place 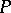 of the base field
of the base field 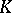 , and
, and 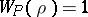 for almost all
for almost all 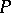 .
.
Interest in root numbers arises in part because they are analogues of Langlands'  -factors appearing in the functional equations of
-factors appearing in the functional equations of 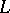 -series associated to automorphic forms. In special settings, global root numbers are known to have deep connections to the vanishing of Dedekind zeta-functions at
-series associated to automorphic forms. In special settings, global root numbers are known to have deep connections to the vanishing of Dedekind zeta-functions at 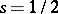 (cf. also Dedekind zeta-function), and to the existence of a global normal integral basis, while local root numbers are connected to Stiefel–Whitney classes, to Hasse symbols of trace forms, and to the existence of a canonical quadratic refinement of the local Hilbert symbol. Excellent references containing both a general account as well as details can be found in [a6], [a11] and [a4].
(cf. also Dedekind zeta-function), and to the existence of a global normal integral basis, while local root numbers are connected to Stiefel–Whitney classes, to Hasse symbols of trace forms, and to the existence of a canonical quadratic refinement of the local Hilbert symbol. Excellent references containing both a general account as well as details can be found in [a6], [a11] and [a4].
Some observations.
a) The global and the local root numbers of 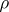 depend only on the isomorphism class of
depend only on the isomorphism class of 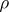 ; hence the root numbers are functions of the character
; hence the root numbers are functions of the character 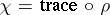 .
.
b) When the character of 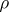 is real-valued, then the global root number
is real-valued, then the global root number 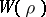 has value
has value 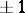 , and each local root number is a fourth root of unity.
, and each local root number is a fourth root of unity.
c) [a1] When 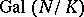 has a representation
has a representation 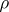 whose character is real-valued and whose global root number
whose character is real-valued and whose global root number 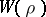 is
is 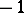 , then the Dedekind zeta-function
, then the Dedekind zeta-function 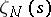 vanishes at
vanishes at 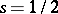 .
.
d) [a5] When 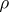 is a real representation (a condition stronger than the requirement that the character be real-valued), then the global root number
is a real representation (a condition stronger than the requirement that the character be real-valued), then the global root number 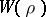 is
is 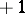 . This means that the product of the local root numbers of a real representation is
. This means that the product of the local root numbers of a real representation is 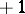 , so the Fröhlich–Queyrut theorem is a reciprocity law (cf. Reciprocity laws), or a "product formula" , for local root numbers. Some authors write "real orthogonal" or just "orthogonal" in place of "real representation" ; all three concepts are equivalent.
, so the Fröhlich–Queyrut theorem is a reciprocity law (cf. Reciprocity laws), or a "product formula" , for local root numbers. Some authors write "real orthogonal" or just "orthogonal" in place of "real representation" ; all three concepts are equivalent.
e) [a12] A normal extension of number fields 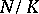 has a normal integral basis if and only if
has a normal integral basis if and only if 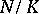 is at most tamely ramified and the global root number
is at most tamely ramified and the global root number  for all irreducible symplectic representations
for all irreducible symplectic representations 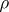 of
of 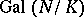 . (By definition, the extension has a normal integral basis provided the ring of integers
. (By definition, the extension has a normal integral basis provided the ring of integers  is a free
is a free 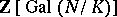 -module).
-module).
f) [a3] Let 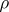 be a real representation and let
be a real representation and let 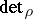 be the
be the 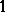 -dimensional real representation obtained by composing
-dimensional real representation obtained by composing 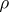 with the determinant. Then for each place
with the determinant. Then for each place 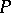 of
of 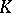 , the normalized local Artin root number
, the normalized local Artin root number 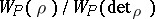 equals the second Stiefel–Whitney class
equals the second Stiefel–Whitney class 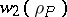 of the restriction of
of the restriction of 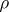 to a decomposition subgroup of
to a decomposition subgroup of 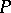 in
in 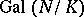 .
.
g) [a9] Let 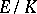 be a finite extension of number fields, with normal closure
be a finite extension of number fields, with normal closure 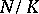 . Let
. Let 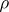 be the representation of
be the representation of 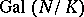 induced by the trivial representation of
induced by the trivial representation of 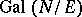 . Then the Hasse symbol
. Then the Hasse symbol 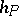 at
at 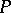 of the trace form
of the trace form  is given by
is given by  , where
, where 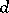 is the discriminant of the trace form and
is the discriminant of the trace form and 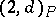 is a Hilbert symbol (cf. Norm-residue symbol).
is a Hilbert symbol (cf. Norm-residue symbol).
h) [a11] For a place 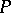 and a non-zero element
and a non-zero element 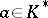 , the
, the 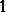 -dimensional real representation
-dimensional real representation 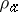 sending
sending 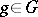 to
to 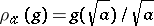 has a local root number
has a local root number 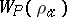 , which will be abbreviated by
, which will be abbreviated by  . For
. For 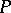 fixed, these local root numbers produce a mapping
fixed, these local root numbers produce a mapping
 |
which satisfies
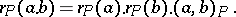 | (a2) |
The last factor is the local Hilbert symbol at 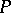 ; it gives a non-degenerate inner product on the local square class group at
; it gives a non-degenerate inner product on the local square class group at 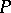 , viewed as a vector space over the field of two elements, the latter identified with
, viewed as a vector space over the field of two elements, the latter identified with 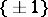 . Equation (a2) has been interpreted in [a7] to mean that the local root numbers give a canonical "quadratic refinement" of this inner product.
. Equation (a2) has been interpreted in [a7] to mean that the local root numbers give a canonical "quadratic refinement" of this inner product.
Remarks.
1) It follows formally from (a1) that 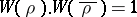 . Moreover,
. Moreover, 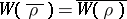 , so the global root number
, so the global root number 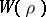 has modulus
has modulus 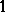 . When the character of
. When the character of 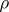 is real-valued, then
is real-valued, then 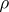 and
and 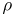 are isomorphic, so their global root numbers are equal:
are isomorphic, so their global root numbers are equal:  . It follows that the global root number
. It follows that the global root number 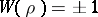 .
.
2) Statement c) follows from the basic argument in [a1], Sect. 3, with minor modifications.
3) To put Taylor's theorem in context, let 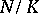 be a finite Galois extension of fields, with Galois group
be a finite Galois extension of fields, with Galois group 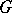 . Then the normal basis theorem of field theory says that
. Then the normal basis theorem of field theory says that 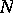 has a
has a 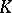 -basis consisting of the Galois conjugates of a single element; restated,
-basis consisting of the Galois conjugates of a single element; restated, 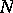 is a free
is a free 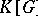 -module. When
-module. When 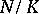 is an extension of number fields, one can ask for a normal integral basis. There are two different notions: One can require the ring of integers
is an extension of number fields, one can ask for a normal integral basis. There are two different notions: One can require the ring of integers 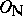 to be a free
to be a free 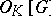 module (necessarily of rank
module (necessarily of rank 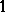 ), or one can require
), or one can require 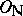 to be a free
to be a free 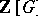 -module (necessarily of rank
-module (necessarily of rank 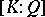 ). These notions coincide when the base field
). These notions coincide when the base field 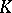 is the field of rational numbers. At present (1998), little is known about the first notion, so the second is chosen. Thus,
is the field of rational numbers. At present (1998), little is known about the first notion, so the second is chosen. Thus, 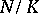 has a normal integral basis when
has a normal integral basis when 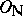 has a
has a 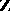 -basis
-basis 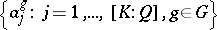 . By results of E. Noether and R. Swan (see [a4], pp. 26–28), a necessary condition for
. By results of E. Noether and R. Swan (see [a4], pp. 26–28), a necessary condition for 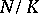 to have a normal integral basis is that
to have a normal integral basis is that 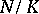 be at most tamely ramified. A. Fröhlich conjectured and M. Taylor proved that the extra conditions beyond tameness needed to make
be at most tamely ramified. A. Fröhlich conjectured and M. Taylor proved that the extra conditions beyond tameness needed to make 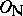 a free
a free  -module is for all the global root numbers of symplectic representations to have value
-module is for all the global root numbers of symplectic representations to have value 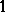 .
.
To say that a complex representation  is symplectic means that the representation has even dimension,
is symplectic means that the representation has even dimension, 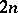 , and factors through the symplectic group
, and factors through the symplectic group 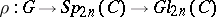 . The character values of a symplectic representation are real. A useful criterion is: When
. The character values of a symplectic representation are real. A useful criterion is: When 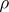 is irreducible with character
is irreducible with character 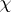 , then the sum
, then the sum
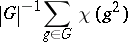 |
takes the value 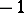 when
when 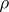 is symplectic, the value
is symplectic, the value 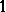 when
when 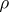 is real, and the value
is real, and the value  in all other cases (see [a10], Prop. 39).
in all other cases (see [a10], Prop. 39).
4) The families of complex numbers which can be realized as the local root numbers of some real representation of the Galois group of some normal extension 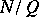 have been determined in [a8].
have been determined in [a8].
References
| [a1] | J.V. Armitage, "Zeta functions with zero at 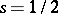 " Invent. Math. , 15 (1972) pp. 199–205 " Invent. Math. , 15 (1972) pp. 199–205 |
| [a2] | P. Deligne, "Les constantes des équation fonctionelles des fonctions 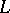 " , Lecture Notes Math. , 349 , Springer (1974) pp. 501–597 " , Lecture Notes Math. , 349 , Springer (1974) pp. 501–597 |
| [a3] | P. Deligne, "Les constantes locales de l'équation fonctionelle des fonction 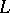 d'Artin d'une répresentation orthogonale" Invent. Math. , 35 (1976) pp. 299–316 d'Artin d'une répresentation orthogonale" Invent. Math. , 35 (1976) pp. 299–316 |
| [a4] | A. Fröhlich, "Galois module structure of algebraic integers" , Ergebn. Math. , 1 , Springer (1983) |
| [a5] | A. Fröhlich, J. Queyrut, "On the functional equation of the Artin L-function for characters of real representations" Invent. Math. , 20 (1973) pp. 125–138 |
| [a6] | J. Martinet, "Character theory and Artin L-functions" , Algebraic Number Fields: Proc. Durham Symp. 1975 , Acad. Press (1977) pp. 1–87 |
| [a7] | R. Perlis, "Arf equivalence I" , Number Theory in Progress: Proc. Internat. Conf. in Honor of A. Schinzel (Zakopane, Poland, June 30--July 9, 1997) , W. de Gruyter (1999) |
| [a8] | R. Perlis, "On the analytic determination of the trace form" Canad. Math. Bull. , 28 : 4 (1985) pp. 422–430 |
| [a9] | J-P. Serre, "L'invariant de Witt de la forme 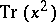 " Comment. Math. Helvetici , 59 (1984) pp. 651–676 " Comment. Math. Helvetici , 59 (1984) pp. 651–676 |
| [a10] | J-P. Serre, "Représentations linéaires des groupes finis" , Hermann (1971) (Edition: Second) |
| [a11] | J. Tate, "Local constants" , Algebraic Number Fields: Proc. Durham Symp. 1975 , Acad. Press (1977) pp. 89–131 |
| [a12] | M. Taylor, "On Fröhlich's conjecture for rings of integers of tame extensions" Invent. Math. , 63 (1981) pp. 41–79 |
Artin root numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artin_root_numbers&oldid=12469