Induced fibre bundle
induced fibration
The fibration  induced by the mapping
induced by the mapping  and the fibration
and the fibration  , where
, where  is the subspace of the direct product
is the subspace of the direct product  consisting of the pairs
consisting of the pairs  for which
for which  , and
, and  is the mapping defined by the projection
is the mapping defined by the projection  . The mapping
. The mapping 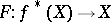 from the induced fibre bundle into the original fibre bundle defined by the formula
from the induced fibre bundle into the original fibre bundle defined by the formula 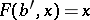 is a bundle morphism covering
is a bundle morphism covering 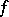 . For each point
. For each point 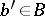 , the restrictions
, the restrictions
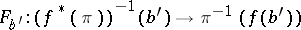 |
are homeomorphisms. Furthermore, for any fibration 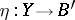 and morphism
and morphism 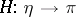 covering
covering 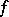 there exist precisely one
there exist precisely one 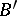 -morphism
-morphism 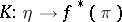 such that
such that 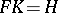 ,
, 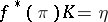 and such that the following diagram is commutative:
and such that the following diagram is commutative: 
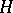
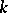
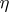

Figure: i050720a
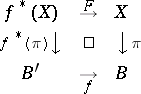 |
Fibre bundles induced from isomorphic fibrations are isomorphic, a fibre bundle induced by a constant mapping is isomorphic to the trivial fibre bundle.
For any section of a fibration 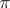 , the mapping
, the mapping 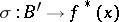 defined by the formula
defined by the formula 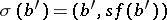 is a section of the induced fibration
is a section of the induced fibration 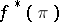 and satisfies the relation
and satisfies the relation 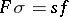 . For example, the mapping
. For example, the mapping  induces the fibration
induces the fibration 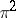 with space
with space 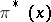 and base
and base  that is the square of the fibration
that is the square of the fibration 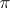 and has the canonical section
and has the canonical section 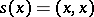 .
.
References
| [1] | C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) |
| [2] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
| [3] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
Induced fibre bundle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Induced_fibre_bundle&oldid=12456