Tensor product
The tensor product of two unitary modules 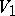 and
and 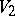 over an associative commutative ring
over an associative commutative ring 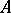 with a unit is the
with a unit is the 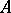 -module
-module 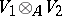 together with an
together with an 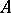 -bilinear mapping
-bilinear mapping
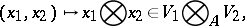 |
which is universal in the following sense: For any 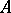 -bilinear mapping
-bilinear mapping 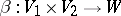 , where
, where 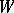 is an arbitrary
is an arbitrary 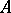 -module, there is a unique
-module, there is a unique 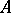 -linear mapping
-linear mapping  such that
such that
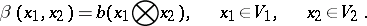 |
The tensor product is uniquely defined up to a natural isomorphism. It always exists and can be constructed as the quotient module of the free  -module
-module  generated by the set
generated by the set 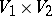 modulo the
modulo the 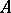 -submodule
-submodule  generated by the elements of the form
generated by the elements of the form
 |
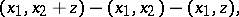 |
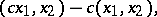 |
 |
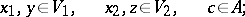 |
then 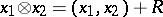 . If one gives up the requirement of commutativity of
. If one gives up the requirement of commutativity of 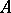 , a construction close to the one described above allows one to form from a right
, a construction close to the one described above allows one to form from a right 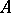 -module
-module 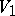 and a left
and a left 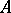 -module
-module 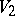 an Abelian group
an Abelian group 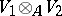 , also called the tensor product of these modules [1]. In what follows
, also called the tensor product of these modules [1]. In what follows 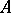 will be assumed to be commutative.
will be assumed to be commutative.
The tensor product has the following properties:
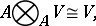 |
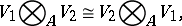 |
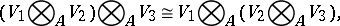 |
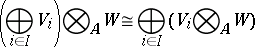 |
for any 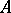 -modules
-modules  ,
,  and
and 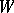 .
.
If  and
and 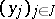 are bases of the free
are bases of the free 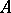 -modules
-modules  and
and 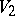 , then
, then 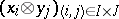 is a basis of the module
is a basis of the module  . In particular,
. In particular,
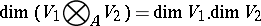 |
if the 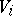 are free finitely-generated modules (for instance, finite-dimensional vector spaces over a field
are free finitely-generated modules (for instance, finite-dimensional vector spaces over a field 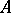 ). The tensor product of cyclic
). The tensor product of cyclic 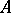 -modules is computed by the formula
-modules is computed by the formula
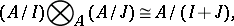 |
where  and
and 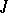 are ideals in
are ideals in  .
.
One also defines the tensor product of arbitrary (not necessarily finite) families of 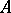 -modules. The tensor product
-modules. The tensor product
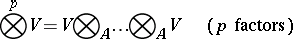 |
is called the 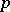 -th tensor power of the
-th tensor power of the  -module
-module 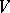 ; its elements are the contravariant tensors (cf. Tensor on a vector space) of degree
; its elements are the contravariant tensors (cf. Tensor on a vector space) of degree  on
on 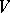 .
.
To any pair of homomorphisms of 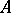 -modules
-modules 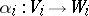 ,
, 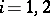 , corresponds their tensor product
, corresponds their tensor product 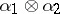 , which is a homomorphism of
, which is a homomorphism of 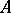 -modules
-modules 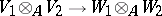 and is defined by the formula
and is defined by the formula
 |
This operation can also be extended to arbitrary families of homomorphisms and has functorial properties (see Module). It defines a homomorphism of 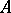 -modules
-modules
 |
 |
which is an isomorphism if all the  and
and 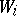 are free and finitely generated.
are free and finitely generated.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [2] | F. Kasch, "Modules and rings" , Acad. Press (1982) (Translated from German) |
| [3] | A.I. Kostrikin, Yu.I. Manin, "Linear algebra and geometry" , Gordon & Breach (1989) (Translated from Russian) |
Comments
An important interpretation of the tensor product in (theoretical) physics is as follows. Often the states of an object, say, a particle, are defined as the vector space 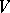 over
over 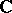 of all complex linear combinations of a set of pure states
of all complex linear combinations of a set of pure states 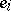 ,
, 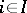 . Let the pure states of a second similar object be
. Let the pure states of a second similar object be 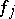 ,
,  , yielding a second vector space
, yielding a second vector space 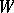 . Then the pure states of the ordered pair of objects are all pairs
. Then the pure states of the ordered pair of objects are all pairs 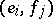 and the space of states of this ordered pair is the tensor product
and the space of states of this ordered pair is the tensor product 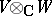 .
.
The tensor product of two algebras 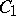 and
and  over an associative commutative ring
over an associative commutative ring 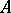 with a unit is the algebra
with a unit is the algebra 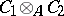 over
over 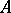 which is obtained by introducing on the tensor product
which is obtained by introducing on the tensor product 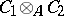 of
of 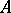 -modules a multiplication according to the formula
-modules a multiplication according to the formula
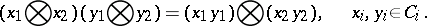 |
This definition can be extended to the case of an arbitrary family of factors. The tensor product 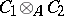 is associative and commutative and contains a unit if both algebras
is associative and commutative and contains a unit if both algebras 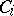 have a unit. If
have a unit. If 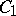 and
and 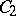 are algebras with a unit over the field
are algebras with a unit over the field 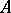 , then
, then 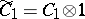 and
and 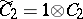 are subalgebras of
are subalgebras of 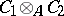 which are isomorphic to
which are isomorphic to  and
and 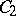 and commute elementwise. Conversely, let
and commute elementwise. Conversely, let 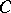 be an algebra with a unit over the field
be an algebra with a unit over the field  , and let
, and let 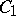 and
and 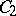 be subalgebras of it containing its unit and such that
be subalgebras of it containing its unit and such that 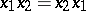 for any
for any 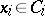 . Then there is a homomorphism of
. Then there is a homomorphism of 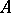 -algebras
-algebras 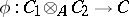 such that
such that 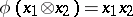 ,
, 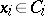 . For
. For 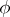 to be an isomorphism it is necessary and sufficient that there is in
to be an isomorphism it is necessary and sufficient that there is in 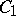 a basis over
a basis over 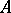 which is also a basis of the right
which is also a basis of the right 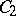 -module
-module 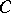 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
The tensor product, or Kronecker product, of two matrices 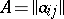 and
and 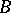 is the matrix
is the matrix
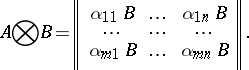 |
Here, 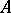 is an
is an 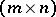 -matrix,
-matrix, 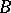 is a
is a 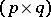 -matrix and
-matrix and 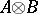 is an
is an 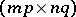 -matrix over an associative commutative ring
-matrix over an associative commutative ring  with a unit.
with a unit.
Properties of the tensor product of matrices are:
 |
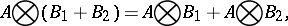 |
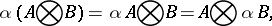 |
where 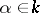 ,
,
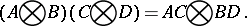 |
If  and
and  , then
, then
 |
Let 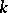 be a field,
be a field,  and
and  . Then
. Then 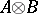 is similar to
is similar to 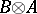 , and
, and  , where
, where 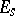 is the unit matrix, coincides with the resultant of the characteristic polynomials of
is the unit matrix, coincides with the resultant of the characteristic polynomials of  and
and 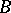 .
.
If  and
and 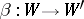 are homomorphisms of unitary free finitely-generated
are homomorphisms of unitary free finitely-generated 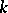 -modules and
-modules and 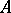 and
and 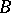 are their matrices in certain bases, then
are their matrices in certain bases, then 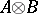 is the matrix of the homomorphism
is the matrix of the homomorphism 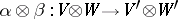 in the basis consisting of the tensor products of the basis vectors.
in the basis consisting of the tensor products of the basis vectors.
References
| [1] | P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958) |
| [2] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
D.A. Suprunenko
The tensor product of two representations 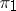 and
and 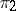 of a group
of a group  in vector spaces
in vector spaces 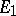 and
and 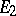 , respectively, is the representation
, respectively, is the representation 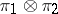 of
of 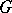 in
in 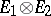 uniquely defined by the condition
uniquely defined by the condition
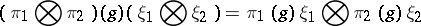 | (*) |
for all 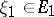 ,
, 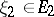 and
and  . If
. If 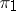 and
and 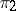 are continuous unitary representations of a topological group
are continuous unitary representations of a topological group 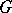 in Hilbert spaces
in Hilbert spaces 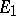 and
and 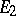 , respectively, then the operators
, respectively, then the operators 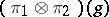 ,
, 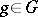 , in the vector space
, in the vector space 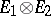 admit a unique extension by continuity to continuous linear operators
admit a unique extension by continuity to continuous linear operators  ,
, 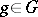 , in the Hilbert space
, in the Hilbert space 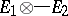 (being the completion of the space
(being the completion of the space 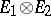 with respect to the scalar product defined by the formula
with respect to the scalar product defined by the formula 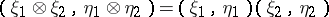 ) and the mapping
) and the mapping 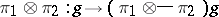 ,
, 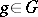 , is a continuous unitary representation of the group
, is a continuous unitary representation of the group 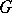 in the Hilbert space
in the Hilbert space  , called the tensor product of the unitary representations
, called the tensor product of the unitary representations 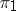 and
and 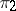 . The representations
. The representations  and
and 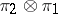 are equivalent (unitarily equivalent if
are equivalent (unitarily equivalent if 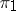 and
and 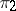 are unitary). The operation of tensor multiplication can be defined also for continuous representations of a topological group in topological vector spaces of a general form.
are unitary). The operation of tensor multiplication can be defined also for continuous representations of a topological group in topological vector spaces of a general form.
A.I. Shtern
Comments
If 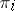 is a representation of an algebra
is a representation of an algebra 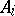 in a vector space
in a vector space 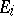 ,
, 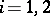 , one defines the tensor product
, one defines the tensor product 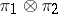 , which is a representation of
, which is a representation of 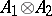 in
in 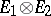 , by
, by
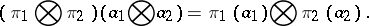 |
In case 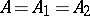 is a bi-algebra (cf. Hopf algebra), composition of this representation with the comultiplication
is a bi-algebra (cf. Hopf algebra), composition of this representation with the comultiplication 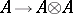 (which is an algebra homomorphism) yields a new representation of
(which is an algebra homomorphism) yields a new representation of 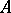 , (also) called the tensor product.
, (also) called the tensor product.
In case 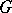 is a group, a representation of
is a group, a representation of 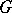 is the same as a representation of the group algebra
is the same as a representation of the group algebra 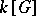 of
of 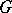 , which is a bi-algebra, so that the previous construction applies, giving the same definition as (*) above. (The comultiplication on
, which is a bi-algebra, so that the previous construction applies, giving the same definition as (*) above. (The comultiplication on 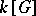 is given by
is given by 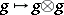 .)
.)
In case 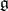 is a Lie algebra, a representation of
is a Lie algebra, a representation of 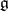 is the same as a representation of its universal enveloping algebra,
is the same as a representation of its universal enveloping algebra, 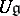 , which is also a bi-algebra (with comultiplication defined by
, which is also a bi-algebra (with comultiplication defined by 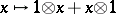 ,
, 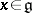 ). This permits one to define the tensor product of two representations of a Lie algebra:
). This permits one to define the tensor product of two representations of a Lie algebra:
 |
The tensor product of two vector bundles 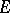 and
and  over a topological space
over a topological space 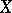 is the vector bundle
is the vector bundle  over
over 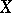 whose fibre at a point
whose fibre at a point 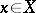 is the tensor product of the fibres
is the tensor product of the fibres 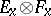 . The tensor product can be defined as the bundle whose transfer function is the tensor product of the transfer functions of the bundles
. The tensor product can be defined as the bundle whose transfer function is the tensor product of the transfer functions of the bundles 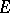 and
and 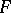 in the same trivializing covering (see Tensor product of matrices, above).
in the same trivializing covering (see Tensor product of matrices, above).
References
| [1] | M.F. Atiyah, "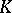 -theory: lectures" , Benjamin (1967) -theory: lectures" , Benjamin (1967) |
Comments
For a vector bundle 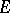 over a space
over a space 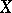 and a vector bundle
and a vector bundle 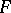 over a space
over a space 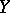 one defines the vector bundle
one defines the vector bundle 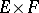 over
over 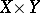 (sometimes written
(sometimes written  ) as the vector bundle over
) as the vector bundle over 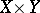 with fibre
with fibre  over
over 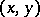 . Pulling back this bundle by the diagonal mapping
. Pulling back this bundle by the diagonal mapping 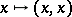 defines the tensor product defined above.
defines the tensor product defined above.
Tensor product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tensor_product&oldid=12437