Differential invariant
An expression composed of one or more functions, their partial derivatives of various orders with respect to independent variables, and sometimes also the differentials of these variables, which is invariant with respect to certain transformations.
Let a geometric object  (cf. Geometric objects, theory of) be given in a differentiable manifold
(cf. Geometric objects, theory of) be given in a differentiable manifold 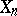 , the elements of which are points
, the elements of which are points 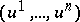 . A geometric object
. A geometric object 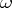 of this manifold is known as a differential invariant of order
of this manifold is known as a differential invariant of order  with respect to the object
with respect to the object  if its coordinates
if its coordinates 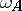 ,
, 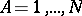 , are functions in the coordinates
, are functions in the coordinates 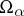 ,
, 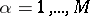 , of
, of  and their partial derivatives with respect to the coordinates
and their partial derivatives with respect to the coordinates 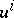 ,
, 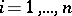 , up to the order
, up to the order  :
:
 |
and have the following property of invariance with respect to coordinate transformations. In fact, under a change of coordinates
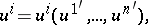 |
the new coordinates 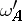 of
of 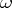 are expressed in terms of the new coordinates
are expressed in terms of the new coordinates 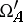 of
of  and their partial derivatives with respect to the new coordinates by means of the same functions
and their partial derivatives with respect to the new coordinates by means of the same functions 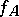 :
:
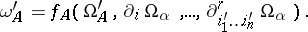 |
For instance, let  be the object of a linear affine (torsion-free) connection. The object
be the object of a linear affine (torsion-free) connection. The object 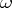 (curvature tensor)
(curvature tensor)
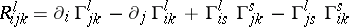 |
is a tensor differential invariant of the first order with respect to the Christoffel symbols 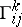 (cf. Christoffel symbol).
(cf. Christoffel symbol).
Let there be given in  a group (pseudo-group)
a group (pseudo-group)  of point transformations
of point transformations
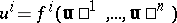 | (1) |
and let  be a submanifold of
be a submanifold of 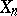 of dimension
of dimension 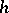 :
:
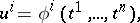 | (2) |
the parameters of which are subject to transformations of the infinite group 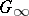 :
:
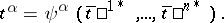 |
A geometric differential invariant of order  of the manifold
of the manifold 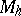 with respect to the group (pseudo-group)
with respect to the group (pseudo-group) 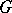 is the name of a function of the coordinates
is the name of a function of the coordinates 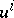 of a point of
of a point of 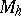 and their partial derivatives up to order
and their partial derivatives up to order  with respect to the parameters
with respect to the parameters 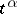 :
:
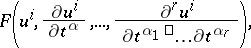 | (3) |
which is invariant with respect to the transformations (1) and (2). In fact, if 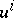 are substituted in (3) according to the formulas (1), while the partial derivatives of
are substituted in (3) according to the formulas (1), while the partial derivatives of 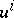 with respect to
with respect to 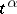 are replaced by their expressions in terms of derivatives of
are replaced by their expressions in terms of derivatives of 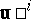 with respect to
with respect to 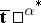 , one obtains the same function
, one obtains the same function 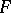 in
in 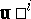 and their derivatives with respect to
and their derivatives with respect to 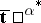 :
:
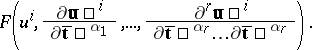 |
If the coordinates 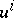 are homogeneous, then
are homogeneous, then 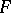 should also be invariant with respect to the transformations
should also be invariant with respect to the transformations
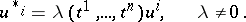 |
In the definition of a geometric differential invariant, 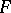 may be replaced by a geometric object. If this object is a covariant (contravariant) vector, it is named covariant (contravariant).
may be replaced by a geometric object. If this object is a covariant (contravariant) vector, it is named covariant (contravariant).
If the vanishing of some object is invariant, the object is named a relative differential invariant.
References
| [1] | T.Y. Thomas, "The differential invariants of generalized spaces" , Cambridge Univ. Press (1934) |
| [2] | R. Weitzenböck, "Invariantentheorie" , Noordhoff (1923) |
Differential invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_invariant&oldid=12434