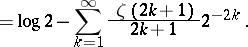Named after its inventor, E.Ch. Catalan (1814–1894), the Catalan constant 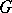 (which is denoted also by
(which is denoted also by 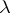 ) is defined by
) is defined by
 | (a1) |
If, in terms of the Digamma (or Psi) function 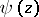 , defined by
, defined by
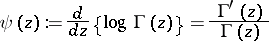 | (a2) |
or
one puts
 | (a3) |
where
then
 | (a4) |
which provides a relationship between the Catalan constant 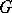 and the Digamma function
and the Digamma function 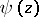 .
.
The Catalan constant 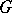 is related also to other functions, such as the Clausen function
is related also to other functions, such as the Clausen function 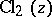 , defined by
, defined by
 | (a5) |
and the Hurwitz zeta-function 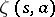 , which is defined, when
, which is defined, when 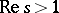 , by
, by
 | (a6) |
Thus,
 | (a7) |
Since
 | (a8) |
the last expression in (a7) would follow also from (a4) in light of the definition in (a3).
A fairly large number of integrals and series can be evaluated in terms of the Catalan constant 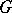 . For example,
. For example,
 | (a9) |
 | (a10) |
and
 | (a11) |
where 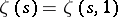 denotes the familiar Riemann zeta-function.
denotes the familiar Riemann zeta-function.
Euler–Mascheroni constant.
Another important mathematical constant is the Euler–Mascheroni constant 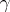 (which is denoted also by
(which is denoted also by 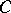 ), defined by
), defined by
 | (a12) |
It is named after L. Euler (1707–1783) and L. Mascheroni (1750–1800). Indeed, one also has
 | (a13) |
and
 | (a14) |
where an empty sum is interpreted, as usual, to be zero. In terms of the Riemann zeta-function 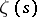 , Euler's classical results state:
, Euler's classical results state:
 | (a15) |
References
| [a1] | A. Erdélyi, W. Magnus, F. Oberhettinger, F.G. Tricomi, "Higher transcendental functions" , I , McGraw-Hill (1953) |
| [a2] | L. Lewin, "Polylogarithms and associated functions" , Elsevier (1981) |
| [a3] | H.M. Srivastava, J. Choi, "Series associated with the zeta and related functions" , Kluwer Acad. Publ. (2001) |
How to Cite This Entry:
Catalan constant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Catalan_constant&oldid=12431
This article was adapted from an original article by Hari M. Srivastava (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article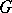 (which is denoted also by
(which is denoted also by 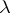 ) is defined by
) is defined by

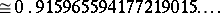
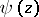 , defined by
, defined by
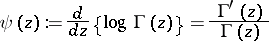
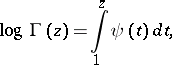

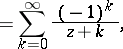
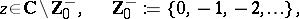

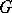 and the Digamma function
and the Digamma function 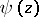 .
.
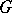 is related also to other functions, such as the Clausen function
is related also to other functions, such as the Clausen function 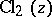 , defined by
, defined by

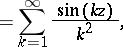
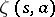 , which is defined, when
, which is defined, when 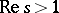 , by
, by

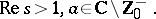

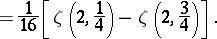

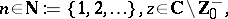
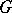 . For example,
. For example,

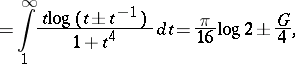

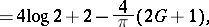

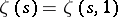 denotes the familiar Riemann zeta-function.
denotes the familiar Riemann zeta-function.
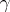 (which is denoted also by
(which is denoted also by 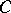 ), defined by
), defined by

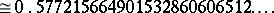

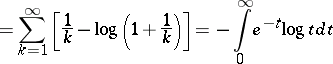

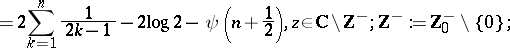
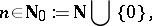
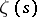 , Euler's classical results state:
, Euler's classical results state: