Topological tensor product

of two locally convex spaces and

A locally convex space having a universality property with respect to bilinear operators on and satisfying a continuity condition. More precisely, let be a certain class of locally convex spaces and for each let there be given a subset of the set of separately-continuous bilinear operators from into . Then the topological tensor product of and 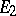(with respect to 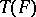) is the (unique) locally convex space 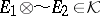together with the operator 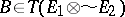having the following property: For any 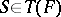, , 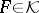there exists a unique continuous linear operator 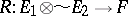such that 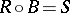. Thus, if one speaks of the functor 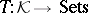, then is defined as the representing object of this functor.

In all known examples 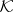contains the field of complex numbers 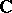, and 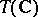contains all bilinear functionals of the form 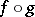, , 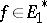, 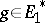mapping 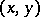to 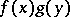. If in this case the topological tensor product exists, then there is a dense subspace in 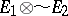that can be identified with the algebraic tensor product 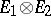; moreover, .

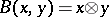If 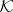consists of all separately (respectively, jointly) continuous bilinear operators, then the topological tensor product is called inductive (respectively, projective). The most important is the projective topological tensor product. Let 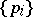be a defining family of semi-norms in 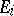, 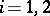; denote by 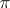the topology on 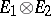defined by the family of semi-norms :

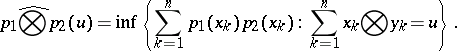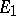If is the class of all, respectively all complete, locally convex spaces, then the projective topological tensor product of and 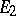exists and its locally convex space is 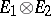with the topology 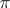, respectively its completion. If the 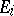are Banach spaces with norms 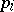, , 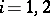then 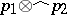is a norm on 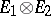; the completion with respect to it is denoted by 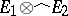. For each 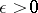the elements of 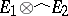have the representation

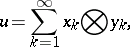where

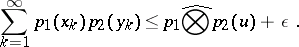If one endows 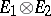with a topology weaker than by using the family of semi-norms ,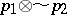

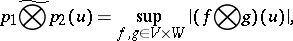where 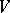and are the polar sets of the unit spheres with respect to 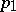and 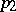, then there arises a topological tensor product, sometimes called injective. The locally convex spaces 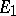with the property that for an arbitrary both topologies in coincide, form the important class of nuclear spaces (cf. Nuclear space).

The projective topological tensor product is associated with the approximation property: A locally convex space 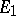has the approximation property if for each pre-compact set 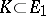and neighbourhood of zero 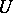there exists a continuous operator of finite rank 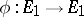such that for all one has . All nuclear spaces have the approximation property. A Banach space 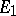has the approximation property if and only if for an arbitrary Banach space 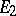the operator 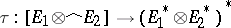, unambiguously defined by the equation 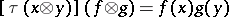, has trivial kernel. A separable Banach space without the approximation property has been constructed [3]. This space also gives an example of a Banach space without a Schauder basis, since the Banach spaces with a Schauder basis have the approximation property (thus S. Banach's so-called "Banach basis problembasis problem" has been negatively solved).

References

[1]	A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires" , Amer. Math. Soc. (1955)
[2]	H.H. Schaefer, "Topological vector spaces" , Macmillan (1966)
[3]	P. Enflo, "A counterexample to the approximation problem in Banach spaces" Acta Math. , 130 (1973) pp. 309–317

References

[a1]	A. Pietsch, "Nukleare lokalkonvexe Räume" , Akademie Verlag (1965)
[a2]	J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , 1. Sequence spaces , Springer (1977)
[a3]	F. Trèves, "Topological vectorspaces, distributions and kernels" , Acad. Press (1967) pp. 198
[a4]	G. Pisier, "Factorisation of linear operators and geometry of Banach spaces" , Amer. Math. Soc. (1986)