Pseudo-differential operator
An operator, acting on a space of functions on a differentiable manifold, that can locally be described by definite rules using a certain function, usually called the symbol of the pseudo-differential operator, that satisfies estimates for the derivatives analogous to the estimates for derivatives of polynomials, which are symbols of differential operators.
Let  be an open set in
be an open set in 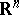 , and let
, and let 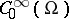 be the space of infinitely-differentiable functions on
be the space of infinitely-differentiable functions on  with compact support belonging to
with compact support belonging to  . The simplest pseudo-differential operator on
. The simplest pseudo-differential operator on  is the operator
is the operator 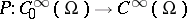 given by
given by
 | (1) |
Here, 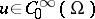 ,
, 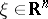 ,
, 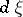 is Lebesgue measure on
is Lebesgue measure on 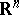 ,
,  is the usual inner product of the vectors
is the usual inner product of the vectors  and
and 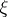 ,
, 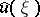 is the Fourier transform of the function
is the Fourier transform of the function  , i.e.
, i.e.
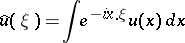 |
(the integral, like the one in (1), is over all of 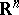 ), and
), and 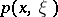 is a smooth function on
is a smooth function on 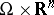 satisfying certain conditions and is called the symbol of the pseudo-differential operator
satisfying certain conditions and is called the symbol of the pseudo-differential operator  (cf. also Symbol of an operator). An operator
(cf. also Symbol of an operator). An operator  of the form (1) is denoted by
of the form (1) is denoted by 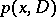 or
or  . If
. If
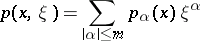 |
is a polynomial in 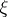 with coefficients
with coefficients  (here
(here 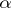 is a multi-index, i.e.
is a multi-index, i.e. 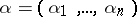 ,
, 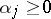 ,
, 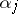 are integers,
are integers, 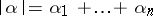 ,
, 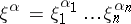 ), then
), then 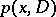 coincides with the differential operator obtained when
coincides with the differential operator obtained when 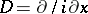 is substituted for
is substituted for 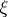 in the expression for
in the expression for 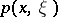 .
.
One often uses the class of symbols 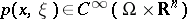 satisfying the conditions
satisfying the conditions
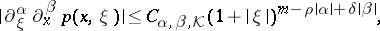 | (2) |
 |
Here 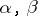 are multi-indices,
are multi-indices, 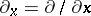 ,
,  , and
, and 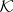 is a compact set in
is a compact set in  . This class is denoted by
. This class is denoted by  (or by
(or by 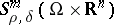 ).
).
It is usually assumed that 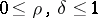 . By
. By 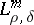 (or
(or 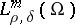 ) one denotes the class of operators of the form
) one denotes the class of operators of the form  , where
, where 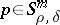 and
and 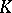 is an integral operator with a
is an integral operator with a 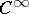 -kernel, i.e. an operator of the form
-kernel, i.e. an operator of the form
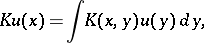 |
where 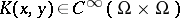 . (Such operators
. (Such operators  are also called pseudo-differential operators in
are also called pseudo-differential operators in  .) The function
.) The function 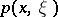 is called, like before, the symbol of
is called, like before, the symbol of  . However, in this case it is not uniquely defined, but only up to a symbol from
. However, in this case it is not uniquely defined, but only up to a symbol from 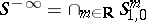 . An operator
. An operator 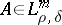 is called a pseudo-differential operator of order not exceeding
is called a pseudo-differential operator of order not exceeding 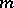 and type
and type 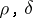 . The differential operator described above belongs to the class
. The differential operator described above belongs to the class 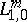 . The smallest possible value of
. The smallest possible value of 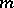 is called the order of the pseudo-differential operator. The classes
is called the order of the pseudo-differential operator. The classes  and
and  are often called the Hörmander classes.
are often called the Hörmander classes.
One may specify pseudo-differential operators in  by double symbols or amplitudes, i.e. write them in the form
by double symbols or amplitudes, i.e. write them in the form
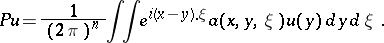 | (3) |
For  this formula turns into (1). It is usually assumed that
this formula turns into (1). It is usually assumed that  , i.e.
, i.e.
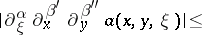 | (4) |
 |
here 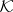 is a compact set in
is a compact set in  . If
. If  , then the class of operators (3) (for all possible functions
, then the class of operators (3) (for all possible functions 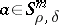 ) coincides with
) coincides with 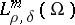 . In this case the symbol
. In this case the symbol 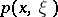 (determined up to a symbol from
(determined up to a symbol from  ) has the following asymptotic expansion:
) has the following asymptotic expansion:
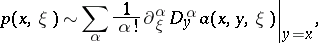 |
where 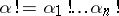 and the summation extends over all multi-indices. This formula means that the difference between
and the summation extends over all multi-indices. This formula means that the difference between 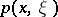 and the partial sum over all
and the partial sum over all 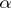 for which
for which 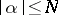 is a symbol in
is a symbol in 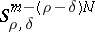 , i.e. is a symbol of order at most equal to the largest of the orders of the rest terms.
, i.e. is a symbol of order at most equal to the largest of the orders of the rest terms.
A pseudo-differential operator 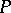 can be extended, by continuity or duality, to an operator
can be extended, by continuity or duality, to an operator  . Here
. Here 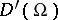 and
and  are the space of generalized functions and the space of generalized functions with compact support in
are the space of generalized functions and the space of generalized functions with compact support in  , respectively (cf. Generalized functions, space of). If
, respectively (cf. Generalized functions, space of). If  , then the pseudo-differential operator has the following pseudo-locality property: If
, then the pseudo-differential operator has the following pseudo-locality property: If 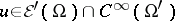 , where
, where  , then
, then 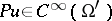 . Another formulation of this property is: The kernel
. Another formulation of this property is: The kernel 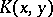 (in the sense of L. Schwartz) of
(in the sense of L. Schwartz) of 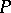 is infinitely differentiable in
is infinitely differentiable in 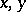 for
for 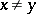 .
.
A classical pseudo-differential operator of order 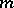 in
in  is an operator
is an operator 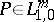 whose symbol
whose symbol 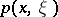 has the asymptotic expansion
has the asymptotic expansion
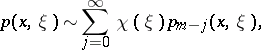 |
where  ,
, 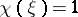 for
for 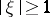 ,
, 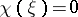 for
for 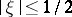 , and where
, and where 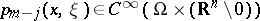 is positively homogeneous in
is positively homogeneous in 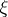 of order
of order 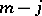 :
:
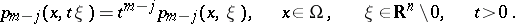 |
A differential operator (with smooth coefficients) serves as an example of a classical pseudo-differential operator. The function  is called the principal symbol of a classical pseudo-differential operator of order
is called the principal symbol of a classical pseudo-differential operator of order 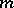 .
.
A pseudo-differential operator 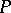 in
in  is called properly supported if the projections of
is called properly supported if the projections of  onto each factor when restricted to the support of the kernel of
onto each factor when restricted to the support of the kernel of 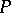 are proper mappings (cf. also Proper morphism). A properly supported pseudo-differential operator maps
are proper mappings (cf. also Proper morphism). A properly supported pseudo-differential operator maps 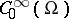 into
into 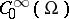 and can be extended, by continuity, to mappings
and can be extended, by continuity, to mappings  ,
, 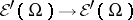 and
and 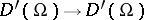 . It can be written in the form (1) with symbol
. It can be written in the form (1) with symbol  , where the exponent is understood as a function of
, where the exponent is understood as a function of  with
with 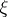 as parameter.
as parameter.
Suppose that 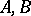 are pseudo-differential operators in
are pseudo-differential operators in  one of which is properly supported. Then their product (composition)
one of which is properly supported. Then their product (composition)  makes sense. The composition theorem plays an important role in the theory of pseudo-differential operators: If
makes sense. The composition theorem plays an important role in the theory of pseudo-differential operators: If  ,
, 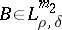 ,
, 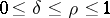 , then
, then  . If, moreover,
. If, moreover, 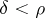 and
and 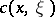 ,
, 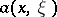 and
and  are the symbols of
are the symbols of 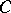 ,
,  and
and 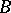 , then
, then
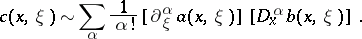 |
In particular, if 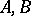 are classical pseudo-differential operators of orders
are classical pseudo-differential operators of orders 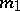 and
and 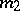 , then
, then 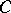 is a classical pseudo-differential operator of order
is a classical pseudo-differential operator of order 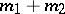 with principal symbol
with principal symbol 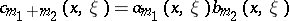 , where
, where 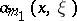 and
and  are the principal symbols of
are the principal symbols of  and
and 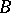 .
.
If 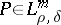 ,
,  , then there exists a, moreover unique, adjoint pseudo-differential operator
, then there exists a, moreover unique, adjoint pseudo-differential operator  for which
for which 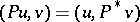 ,
, 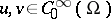 , where
, where 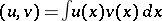 is the inner product of
is the inner product of  and
and  in
in 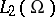 . If, moreover,
. If, moreover, 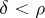 ,
, 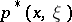 is the symbol of
is the symbol of 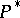 and
and 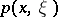 is the symbol of
is the symbol of 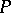 , then
, then
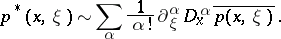 |
Thus, the properly supported pseudo-differential operators for 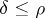 form an algebra with involution given by transition to the adjoint operator. The arbitrary pseudo-differential operators form a module over this algebra.
form an algebra with involution given by transition to the adjoint operator. The arbitrary pseudo-differential operators form a module over this algebra.
The theorem on the boundedness of pseudo-differential operators from the Hörmander classes in the 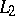 -norm, in its most precise form, asserts the following (cf. [8]): Let
-norm, in its most precise form, asserts the following (cf. [8]): Let 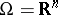 and let
and let 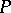 be an operator of the form (3) with double symbol
be an operator of the form (3) with double symbol 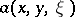 satisfying (4), in which the numbers
satisfying (4), in which the numbers  satisfy the conditions
satisfy the conditions
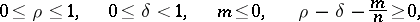 | (5) |
then 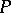 can be extended to a bounded operator
can be extended to a bounded operator 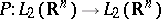 . In particular, under the conditions (5) pseudo-differential operators of the form (1) with symbols satisfying conditions (2) uniformly in
. In particular, under the conditions (5) pseudo-differential operators of the form (1) with symbols satisfying conditions (2) uniformly in  (i.e. such that the constants
(i.e. such that the constants 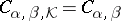 do not depend on
do not depend on 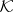 ) are bounded in
) are bounded in 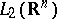 . This implies, e.g., the boundedness in
. This implies, e.g., the boundedness in 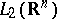 of operators
of operators 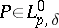 if
if  and if the kernel of
and if the kernel of  has compact support (when the bounds on the symbol are, again, uniform in
has compact support (when the bounds on the symbol are, again, uniform in  ). For
). For 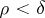 or for
or for  , operators of such a form need not be bounded [19a]. Analogously, in general, if one of the two latter conditions of (5) are not fulfilled, then one already obtains a class of pseudo-differential operators that contains unbounded ones.
, operators of such a form need not be bounded [19a]. Analogously, in general, if one of the two latter conditions of (5) are not fulfilled, then one already obtains a class of pseudo-differential operators that contains unbounded ones.
In terms of bounds on symbols one can give conditions for the boundedness of pseudo-differential operators in 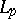 -norms, as well as in Hölder and in Gevrey norms (cf. [8]).
-norms, as well as in Hölder and in Gevrey norms (cf. [8]).
If an operator 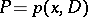 is given on
is given on 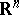 , where
, where 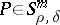 ,
,  and where (2) holds uniformly in
and where (2) holds uniformly in  , then this operator can be extended to a bounded operator
, then this operator can be extended to a bounded operator  ,
, 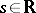 , where
, where  denotes the usual Sobolev space over
denotes the usual Sobolev space over 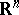 (which is sometimes denoted also by
(which is sometimes denoted also by  ).
).
The class of pseudo-differential operators in  for
for 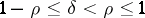 is naturally invariant under diffeomorphisms. Its subclass of classical pseudo-differential operators has the same property. This makes it possible to define the class
is naturally invariant under diffeomorphisms. Its subclass of classical pseudo-differential operators has the same property. This makes it possible to define the class 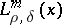 and classical pseudo-differential operators on an arbitrary smooth manifold
and classical pseudo-differential operators on an arbitrary smooth manifold  . The formula for change of variables in the symbol under a diffeomorphism
. The formula for change of variables in the symbol under a diffeomorphism 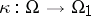 , where
, where 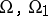 are domains in
are domains in 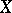 , has the form
, has the form
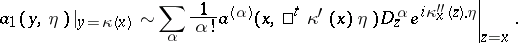 |
Here 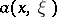 is the symbol of
is the symbol of 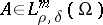 ;
; 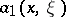 is the symbol of the operator
is the symbol of the operator 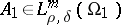 given by
given by 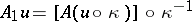 , i.e. that obtained from
, i.e. that obtained from  by a change of variables
by a change of variables 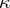 ;
;  denotes the Jacobian of
denotes the Jacobian of 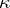 ;
; 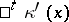 is the transposed matrix; and
is the transposed matrix; and
 |
In particular, this implies that the principal symbol of a classical pseudo-differential operator on a manifold  is a well-defined function on the cotangent bundle
is a well-defined function on the cotangent bundle 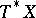 .
.
If  is a compact manifold (without boundary), then the pseudo-differential operators on
is a compact manifold (without boundary), then the pseudo-differential operators on  form an algebra with involution, if the involution is introduced by means of an inner product, given by a smooth positive density. An operator
form an algebra with involution, if the involution is introduced by means of an inner product, given by a smooth positive density. An operator 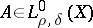 is bounded in
is bounded in 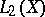 , and if
, and if  for
for  , then it is compact in
, then it is compact in 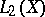 . For classical pseudo-differential operators
. For classical pseudo-differential operators  of order
of order  on
on  ,
,
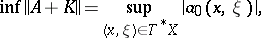 |
where 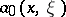 is the principal symbol of
is the principal symbol of  and
and 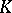 runs over the set of compact operators in
runs over the set of compact operators in 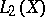 . An operator
. An operator  can by continuity be extended to a bounded linear operator from
can by continuity be extended to a bounded linear operator from  into
into 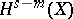 for any
for any 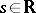 .
.
A parametrix of a pseudo-differential operator  is a pseudo-differential operator
is a pseudo-differential operator 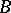 such that
such that 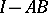 and
and 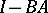 are pseudo-differential operators of order
are pseudo-differential operators of order 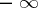 , i.e. are integral operators with a smooth kernel. Suppose that
, i.e. are integral operators with a smooth kernel. Suppose that 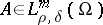 ,
, 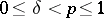 , and that
, and that 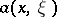 is the symbol of
is the symbol of 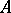 . A sufficient condition for
. A sufficient condition for  to have a parametrix is that the conditions
to have a parametrix is that the conditions
 | (6) |
are fulfilled.
In this case a parametrix  exists. The simplest implication from the existence of a parametrix is that
exists. The simplest implication from the existence of a parametrix is that  is a hypo-elliptic operator: If
is a hypo-elliptic operator: If  , where
, where  , then
, then 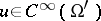 . In other words,
. In other words, 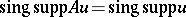 (cf. Support of a generalized function). The following exact result (the regularity theorem) is also valid: If
(cf. Support of a generalized function). The following exact result (the regularity theorem) is also valid: If 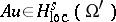 , then
, then 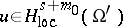 . A micro-local regularity theorem is also valid:
. A micro-local regularity theorem is also valid: 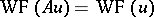 , where
, where 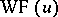 denotes the wave front of the generalized function
denotes the wave front of the generalized function  .
.
Condition (6) is invariant under diffeomorphisms for 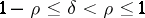 . Therefore the corresponding class of pseudo-differential operators on a manifold
. Therefore the corresponding class of pseudo-differential operators on a manifold 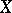 has a meaning. If
has a meaning. If  is compact, then such an operator
is compact, then such an operator  is Fredholm in
is Fredholm in 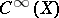 (cf. Fredholm operator), i.e. has finite-dimensional kernel and co-kernel in
(cf. Fredholm operator), i.e. has finite-dimensional kernel and co-kernel in 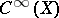 , and has a closed image.
, and has a closed image.
A classical pseudo-differential operator  of order
of order 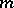 with smooth symbol
with smooth symbol 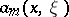 is called elliptic if
is called elliptic if 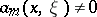 for
for 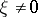 . For such an operator
. For such an operator  condition (6) holds with
condition (6) holds with 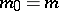 , and
, and  has a parametrix that is also a classical pseudo-differential operator of order
has a parametrix that is also a classical pseudo-differential operator of order 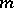 . On a compact manifold
. On a compact manifold  such an operator
such an operator  gives rise to a Fredholm operator
gives rise to a Fredholm operator
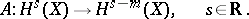 |
All these definitions and statements can be transferred to pseudo-differential operators acting on vector functions, or, more generally, on sections of vector bundles. For an elliptic operator on a compact manifold  the index of the mapping
the index of the mapping 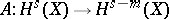 determined by it on the Sobolev classes of sections does not depend on
determined by it on the Sobolev classes of sections does not depend on 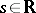 and can be explicitly computed (cf. Index formulas).
and can be explicitly computed (cf. Index formulas).
The role of pseudo-differential operators lies in the fact that there is a number of operations leading outside the class of differential operators but preserving the class of pseudo-differential operators. E.g., the resolvent and complex powers of an elliptic differential operator on a compact manifold are classical pseudo-differential operators; they arise when reducing an elliptic boundary value problem to the boundary (cf., e.g., [7], [8], and [1e]).
There are several versions of the theory of pseudo-differential operators, adapted to the solution of various problems in analysis and mathematical physics. Often, pseudo-differential operators with a parameter arise; they are necessary, e.g., in the study of resolvent and asymptotic expansions for eigen values. An important role is played by different versions of the theory of pseudo-differential operators in 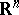 , taking into account effects related to the description of the behaviour of functions at infinity, and often inspired by mathematical problems in quantum mechanics arising in the study of quantization of classical systems (cf. [5], [11]). In the theory of local solvability of partial differential equations and in spectral theory it is expedient to use pseudo-differential operators whose behaviour can be described by weight functions replacing
, taking into account effects related to the description of the behaviour of functions at infinity, and often inspired by mathematical problems in quantum mechanics arising in the study of quantization of classical systems (cf. [5], [11]). In the theory of local solvability of partial differential equations and in spectral theory it is expedient to use pseudo-differential operators whose behaviour can be described by weight functions replacing 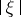 in estimates of the type (2) (cf. [8], [14]). One has constructed an algebra of pseudo-differential operators on manifolds with boundary, containing, in particular, the parametrix of elliptic boundary value problems (cf. [3], [13]).
in estimates of the type (2) (cf. [8], [14]). One has constructed an algebra of pseudo-differential operators on manifolds with boundary, containing, in particular, the parametrix of elliptic boundary value problems (cf. [3], [13]).
A particular case of pseudo-differential operators are the multi-dimensional singular integral and integro-differential operators, whose study prepared the emergence of the theory of pseudo-differential operators (cf. [12] and also Singular integral).
The theory of pseudo-differential operators serves as a basis for the study of Fourier integral operators (cf. Fourier integral operator; [7], [10]), which play the same role in the theory of hyperbolic equations as do pseudo-differential operators in the theory of elliptic equations.
References
| [1a] | J.J. Kohn, L. Nirenberg, "An algebra of pseudo-differential operators" Commun. Pure Appl. Math. , 18 : 1–2 (1965) pp. 269–305 |
| [1b] | L. Hörmander, "Pseudo-differential operators" Commun. Pure Appl. Math. , 18 : 3 (1965) pp. 501–517 |
| [1c] | J.J. Kohn, L. Nirenberg, "Non-coercive boundary value problems" Commun. Pure Appl. Math. , 18 : 3 (1965) pp. 443–492 |
| [1d] | L. Hörmander, "Pseudo-differential operators and non-elliptic boundary problems" Ann. of Math. , 83 : 1 (1966) pp. 129–209 |
| [1e] | L. Hörmander, "Pseudo-differential operators and hypoelliptic equations" A.P. Calderòn (ed.) , Singular Integrals , Proc. Symp. Pure Math. , 10 , Amer. Math. Soc. (1966) pp. 138–183 |
| [2] | M.S. Agranovich, M.I. Vishik, "Pseudo-differential operators" , Moscow (1988) (In Russian) |
| [3] | G.I. Eskin, "Boundary value problems for elliptic pseudodifferential equations" , Amer. Math. Soc. (1981) (Translated from Russian) |
| [4] | V.V. Grushin, "Pseudodifferential operators" , Moscow (1975) (In Russian) |
| [5] | M.A. Shubin, "Pseudo-differential operators and spectral theory" , Springer (1987) (Translated from Russian) |
| [6] | K.O. Friedrichs, "Pseudo-differential operators" , Courant Inst. Math. (1970) |
| [7] | F. Trèves, "Introduction to pseudo-differential and Fourier integral operators" , 1–2 , Plenum (1980) |
| [8] | M.E. Taylor, "Pseudo-differential operators" , Springer (1974) |
| [9] | H. Kumanogo, "Pseudo-differential operators" , M.I.T. (1981) |
| [10] | J.J. Duistermaat, "Fourier integral operators" , Courant Inst. Math. (1973) |
| [11] | V.P. Maslov, M.V. Fedoryuk, "Quasi-classical approximation for the equations of quantum mechanics" , Reidel (1981) (Translated from Russian) |
| [12] | M.S. Agranovich, "Elliptic singular integro-differential operators" Russian Math. Surveys , 20 : 5 (1965) pp. 1–121 Uspekhi Mat. Nauk , 20 : 5 (1965) pp. 3–120 |
| [13] | L. Boutet de Monvel, "Boundary value problems for pseudodifferential operators" Acta Math. , 126 (1971) pp. 11–51 |
| [14] | L. Hörmander, "The Weyl calculus of pseudo-differential operators" Commun. Pure Appl. Math. , 32 : 3 (1979) pp. 359–443 |
| [15a] | H.O. Cordes, "Elliptic pseudo-differential operators - an abstract theory" , Lect. notes in math. , 756 , Springer (1979) |
| [15b] | H.O. Cordes, "Spectral theory of linear differential operators and comparison algebras" , Cambridge Univ. Press (1986) |
| [16] | Yu.V. Egorov, "Linear differential equations of principal type" , Consultants Bureau (1986) (Translated from Russian) |
| [17] | G. Grubb, "Functional calculus of pseudo-differential boundary problems" , Birkhäuser (1986) |
| [18] | B. Helffer, "Théorie spectrale pour des opérateurs globalement elliptiques" Astérisque , 112 (1984) |
| [19a] | L. Hörmander, "Pseudo-differential operators of type 1,1" Comm. Partial Diff. Eq. , 13 : 9 (1988) pp. 1085–1111 |
| [19b] | L. Hörmander, "Continuity of pseudo-differential operators of type 1,1" Comm. Partial Diff. Eq. , 14 : 2 (1989) pp. 231–243 |
| [20] | V. Ivrii, "Precise spectral asymptotics for elliptic operators" , Lect. notes in math. , 1100 , Springer (1984) |
| [21] | S. Rempel, B.-W. Schulze, "Index theory of elliptic boundary problems" , Akademie Verlag (1982) |
Comments
The phrase "pseudo-differential operator" is often abbreviated to 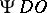 , just like
, just like 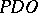 for "partial differential operator" .
for "partial differential operator" .
For algebras of  on manifolds with singularities, in particular
on manifolds with singularities, in particular  with discontinuous symbols, see [a2].
with discontinuous symbols, see [a2].
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1–4 , Springer (1983–1985) |
| [a2] | B.A. Plamenevskii, "Algebras of pseudodifferential operators" , Kluwer (1989) (Translated from Russian) |
| [a3] | M.E. Taylor, "Pseudo-differential operators" , Princeton Univ. Press (1981) |
| [a4] | J. Chazarain, A. Piriou, "Introduction to the theory of linear partial differential equations" , North-Holland (1982) (Translated from French) |
Pseudo-differential operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-differential_operator&oldid=12424