Isogeny
An epimorphism of group schemes (cf. Group scheme) with a finite kernel. A morphism  of group schemes over a ground scheme
of group schemes over a ground scheme  is said to be an isogeny if
is said to be an isogeny if  is surjective and if its kernel
is surjective and if its kernel  is a flat finite group
is a flat finite group  -scheme.
-scheme.
In what follows it is assumed that 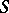 is the spectrum of a field
is the spectrum of a field  of characteristic
of characteristic  . Suppose that
. Suppose that 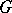 is a group scheme of finite type over
is a group scheme of finite type over 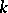 , and let
, and let 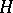 be a finite subgroup scheme. Then the quotient
be a finite subgroup scheme. Then the quotient  exists, and the natural mapping
exists, and the natural mapping  is an isogeny. Conversely, if
is an isogeny. Conversely, if 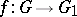 is an isogeny of group schemes of finite type and
is an isogeny of group schemes of finite type and  , then
, then  . For every isogeny
. For every isogeny 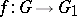 of Abelian varieties there exists an isogeny
of Abelian varieties there exists an isogeny  such that the composite
such that the composite 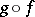 is the homomorphism
is the homomorphism  of multiplication of
of multiplication of 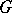 by
by  . Composites of isogenies are isogenies. Two group schemes
. Composites of isogenies are isogenies. Two group schemes  and
and 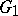 are said to be isogenous if there exists an isogeny
are said to be isogenous if there exists an isogeny 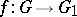 . An isogeny
. An isogeny 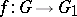 is said to be separable if
is said to be separable if 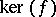 is an étale group scheme over
is an étale group scheme over  . This is equivalent to the fact that
. This is equivalent to the fact that  is a finite étale covering. An example of a separable isogeny is the homomorphism
is a finite étale covering. An example of a separable isogeny is the homomorphism  , where
, where 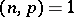 . If
. If 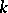 is a finite field, then every separable isogeny
is a finite field, then every separable isogeny 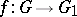 of connected commutative group schemes of dimension one factors through the isogeny
of connected commutative group schemes of dimension one factors through the isogeny 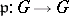 , where
, where 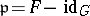 and
and  is the Frobenius endomorphism. An example of a non-separable isogeny is the homomorphism of multiplication by
is the Frobenius endomorphism. An example of a non-separable isogeny is the homomorphism of multiplication by 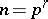 in an Abelian variety
in an Abelian variety  .
.
Localization of the additive category 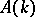 of Abelian varieties over
of Abelian varieties over  with respect to isogeny determines an Abelian category
with respect to isogeny determines an Abelian category 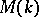 , whose objects are called Abelian varieties up to isogeny. Every such object can be identified with an Abelian variety
, whose objects are called Abelian varieties up to isogeny. Every such object can be identified with an Abelian variety  , and the morphisms
, and the morphisms 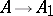 in
in  are elements of the algebra
are elements of the algebra  over the field of rational numbers. An isogeny
over the field of rational numbers. An isogeny  defines an isomorphism of the corresponding objects in
defines an isomorphism of the corresponding objects in 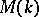 . The category
. The category 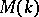 is semi-simple: each of its objects is isomorphic to a product of indecomposable objects. There is a complete description of
is semi-simple: each of its objects is isomorphic to a product of indecomposable objects. There is a complete description of  when
when 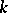 is a finite field (see [4]).
is a finite field (see [4]).
The concept of an isogeny is also defined for formal groups. A morphism 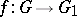 of formal groups over a field
of formal groups over a field 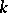 is said to be an isogeny if its image in the quotient category
is said to be an isogeny if its image in the quotient category  of the category of formal groups over
of the category of formal groups over 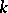 by the subcategory of Artinian formal groups is an isomorphism. An isogeny of group schemes determines an isogeny of the corresponding formal completions. There is a description of the category
by the subcategory of Artinian formal groups is an isomorphism. An isogeny of group schemes determines an isogeny of the corresponding formal completions. There is a description of the category 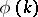 of formal groups up to isogeny (see [1], [2]).
of formal groups up to isogeny (see [1], [2]).
References
| [1] | Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" Russian Math. Surveys , 18 : 6 (1963) pp. 1–81 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 3–90 |
| [2] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) |
| [3] | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) |
| [4] | J.T. Tate, "Classes d'isogénie des variétés abéliennes sur un corps fini (d' après T. Honda)" , Sem. Bourbaki Exp. 352 , Lect. notes in math. , 179 , Springer (1968/69) |
| [5] | J. Dieudonné, "Groupes de Lie et hyperalgèbres de Lie sur un corps de characteristique 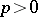 " Comm. Math. Helvetici , 28 : 1 (1954) pp. 87–118 " Comm. Math. Helvetici , 28 : 1 (1954) pp. 87–118 |
Comments
References
| [a1] | T. Honda, "Isogeny classes of Abelian varieties over finite fields" Math. Soc. Japan , 20 (1968) pp. 83–95 |
| [a2] | J. Tate, "Endomorphisms of Abelian varieties over finite fields" Invent. Math. , 2 (1966) pp. 134–144 |
Isogeny. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isogeny&oldid=12388